Определение критической силы

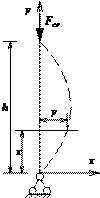Рассмотрим стержень с шарнирно закрепленными концами, нагруженный силой 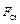(рис. 28.1.1). Под действием критической силы 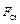стержень потерял устойчивость. Дифференциальное уравнение его изогнутой оси имеет вид:

(28.1.1)

где M_x = F _cr y – изгибающий момент в сечении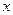

или

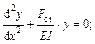
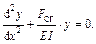(28.1.2)

Обозначив

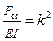, (28.1.3)

получим однородное дифференциальное уравнение второго порядка:

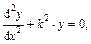
решение которого имеет вид:

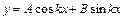, (28.1.4)

где А и В – постоянные интегрирования, которые определяются из граничных условий.

Запишем граничные условия для заданного стержня в выбранной системе координат (рис. 28.1.1):

а) x = 0; y = 0;

б) x = l; y = 0;

или

а)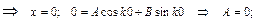

б) .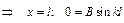

В не может быть равно нулю, т. к. в этом случае задача не имеет смысла, следовательно,

sin kl = 0, или kl = π n, (28.1.5)

где n = 0, 1, 2…

Подставляя (28.1.5) в (28.1.3), имеем

,

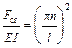тогда

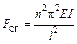(28.1.6)

Наименьшее значение сила 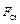имеет, если п = 1; 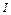=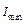, окончательно:

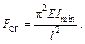(28.1.7)

Эта формула была получена в 1744 г. Леонардом Эйлером и носит название формулы Эйлера для определения величины критической силы, когда у стержня концы шарнирно закреплены, т. е. когда при потере устойчивости его ось образует одну полуволну синусоиды.

Рассмотрим влияние способа закрепления концов стержня на величину критической силы.

Повторив решение дифференциального уравнения (28.1.1) при других граничных условиях (рис. 28.1.2), получим формулы:

; ; .

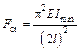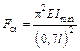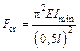Тогда формулу Эйлера можно записать в более общем виде:

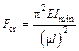, (28.1.8)

где – коэффициент привидения длины; 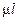– приведенная длина.

Рис. 28.1.2

Из рис. 28.1.1 и 28.1.2 видно, что

= 1, если концы стержня шарнирно закреплены (рис. 28.1.1);

= 2, если один конец защемлен, а второй свободен (рис. 28.1.2, а);

= 0,7, если один конец закреплен, а второй шарнирно оперт (рис. 28.1.2, б);

= 0,5, если оба конца защемлены (рис. 28.1.2, в).

Дата добавления: 2014-01-07