При циклически меняющихся напряжениях

Расчеты на прочность

Расчеты прочности деталей, в которых возникают циклически меняющиеся напряжения, обычно начинают со статического расчета по пониженным допускаемым напряжениям. Этот расчет служит для предварительного определения размеров и конфигурации детали.

После выполнения рабочего чертежа производят проверочный расчет. Для этого определяют коэффициенты ε, k и β.

Сам проверочный расчет заключается в определении фактического коэффициента запаса прочности п и сравнении его с допускаемым 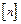т. е. в этом случае условие прочности имеет вид:

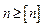. (30.4.1)

Если фактический коэффициент запаса прочности ниже допускаемого, то прочность недостаточна, а если значительно выше, то деталь тяжела и неэкономична. Как в первом, так и во втором случае приходится вносить те или иные изменения в конструкцию детали и повторять проверочный расчет.

Рассмотрим определение фактического коэффициента запаса прочности в случае линейного напряженного состояния, которое возникает при чистом изгибе и при растяжении-сжатии.

Обычно коэффициент запаса прочности п определяют, полагая предельный цикл напряжений подобным рабочему. При этом предположении коэффициент запаса прочности представляет собой отношение предела выносливости, определенного для детали при данном виде деформации и характеристике цикла, к номинальному значению максимального напряжения, возникающего в рассчитываемой точке детали, т. е.

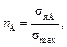(30.4.2)

где 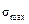– номинальное значение напряжения.

Его определяют по основным формулам сопротивления материалов, т. е. без учета концентрации напряжений.

В случае симметричного цикла предел выносливости для детали

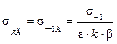, (30.4.3)

тогда

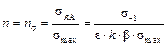. (30.4.4)

Учитывая, что при симметричном цикле 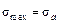, получим следующее выражение для коэффициента запаса прочности:

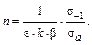(30.4.5)

В случае асимметричного цикла предел выносливости детали 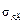определяют по схематизированной диаграмме предельных амплитуд (рис. 30.3.1). Эта диаграмма отличается от ранее рассмотренной тем, что она построена не для лабораторного образца, а для действительной детали. т. е. ордината точки А равна не 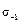, а .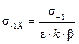

Абсцисса точки В, равная S, не изменяется и для детали, так как абсолютные размеры детали, концентрация напряжений и состояние поверхности почти не сказываются на величине предела прочности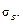

Предположим, что рабочий цикл напряжений в опасной точке сечения детали на диаграмме предельных амплитуд определяется точкой М с координатами σ _т и σ _а (рис. 30.4.1). Тогда предельный цикл, подобный данному, т. е. с тем же коэффициентом асимметрии R, будет определяться точкой F, полученной от пересечения прямой ОМ с линией предельных амплитуд. Координаты точки F в выбранном масштабе равны средним напряжениям σ _{m пр} и амплитуде предельного цикла σ_апр.

В этом случае максимальное напряжение предельного цикла, представляющее предел выносливости детали, будет

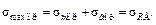(30.4.6)

Коэффициент запаса прочности

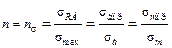(30.4.7)

Из подобия треугольников ОАВ и ЕFВ имеем:,

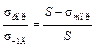откуда

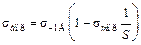. (30.4.8)

Из уравнения (30.4.7)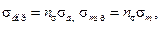

тогда

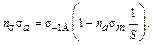(30.4.9)

Из уравнения (31.3.9) находим коэффициент запаса прочности:

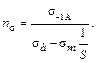(30.4.10)

Выражение (30.4.10) может быть использовано для определения коэффициента запаса прочности при известных величинах предела выносливости детали для симметричного цикла 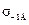, среднего напряжения 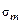и амплитуды цикла напряжений 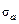в опасной точке.

В случае, когда в поперечных сечениях детали возникают циклически меняющиеся касательные напряжения, например, при кручении, коэффициент запаса прочности будет

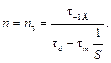, (30.3.11)

где 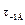– предел выносливости детали при симметричном цикле при кручении (определяется как и 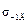только величины коэффициентов ε, k и β будут иными); и 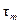– амплитуда и среднее напряжение заданного рабочего цикла в опасной точке.

Если в поперечном сечении детали возникают циклически меняющиеся нормальные и касательные напряжения, например, при изгибе с кручением, то коэффициент запаса прочности:

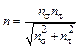, (30.4.12)

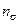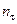где и – коэффициенты запаса прочности только при изгибе и только при кручении, определяемые по формулам (30.4.10) и (30.4.11).

ЗАКЛЮЧЕНИЕ

Закончив рассмотрение методов расчета элементов сооружений на прочность, жесткость и устойчивость, студент может считать себя подготовленным к изучению специальных дисциплин: строительной механики, строительных конструкций.

В представленном курсе лекций объектом рассмотрения являлся брус (балка, стержень); в расчетах использовались простейшие модели, описывающие свойства материалов. В то же время, например, новые композиционные материалы иногда не могут быть описаны с помощью рассмотренной выше модели однородного сплошного тела. Технология изготовления материалов и взаимодействие их с окружающей средой требуют углубленного развития теории.

Строительные конструкции представляют собой сложные многоэлементные системы, в которых требуется учитывать одновременно физическую и геометрическую нелинейность сооружения как единого целого. Анализ отдельного элемента часто является недостаточным. Это возможно лишь с использованием вычислительной техники высокого уровня. Поэтому в сопротивлении материалов, как и в целом в механике деформируемого тела, постоянную актуальность сохраняет проблема развития эффективных численных методов.

Далеко не все проблемы могут быть решены расчетом. Эксперимент по-прежнему играет важную роль в вопросах прочности и деформирования.

Здесь представлен далеко не полный перечень проблем, которые предстоит решать инженеру в его практической деятельности. Но даже из этого краткого перечня очевидна исключительно важная роль сопротивления материалов в деле создания экономичных и долговечных сооружений настоящего и будущего.

Представленный курс лекций по сопротивлению материалов будет полезен студентам при выполнении расчетно-графических заданий, контрольных работ, а также при подготовке к экзаменам

Дата добавления: 2014-01-07