Понятие и вероятностный смысл математического ожидания дискретной случайной величины

Как уже известно, закон распределения пол­ностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничи­ваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожи­дание.

Математическое ожидание, как будет показано далее, приближенно равно среднему значению случайной вели­чины. Для решения многих задач достаточно знать мате­матическое ожидание. Например,если известно, что мате­матическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в сред­нем выбивает больше очков, чем второй, и, следова­тельно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.

Математическое ожидание дискретной случайной величины

Математическим ожиданием дискретной слу­чайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Если дискретная случайная величина Х принимает счетное множество возможных значений, то

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Замечание.Из определения следует, что математическое ожиданиедискретной случайной величины есть неслучайная (постоянная) величина. Рекомендуется запомнить это утверждение, так как далее оно используется многократно. В дальнейшем будет пока­зано, что математическое ожидание непрерывной случайной величины также есть постоянная величина.

Пример 1. Найти математическое ожидание случайной вели­чины X. зная закон ее распределения:

Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:

М (Х}==3.0,1 +5.0,6+2.0,3==3,9.

Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.

Решение. Случайная величина Х— число появлений события

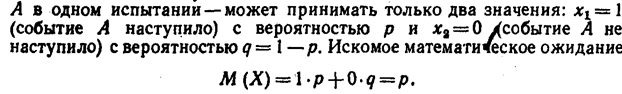
Итак, математическое ожидание числа появлений собы­тия в одном испытании равно вероятности этого собы­тия.Этот результат будет использован далее (ниже).

Дата добавления: 2014-01-07