Среднеквадратическое отклонение одной и суммы независимых случайных величин

Итак,

Свойства дисперсии и их следствия.

Свойство 1.

Дисперсия постоянной величины С равна нулю:

Доказательство. По определению дисперсии,

Пользуясь первым свойством математического ожида­ния (математическое ожидание постоянной равно самой постоянной), получим

Свойство становится ясным, если учесть, что постоян­ная величина сохраняет одно и то же значение и рассея­ния, конечно, не имеет.

Свойство 2.

Постоянный множитель можно выно­сить за знак дисперсии, возводя его в квадрат:

Доказательство.

По определению дисперсии имеем

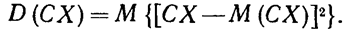
Пользуясь вторым свойством математического ожида­ния (постоянный множитель можно выносить за знак математического ожидания), получим

Итак,

Свойство становится ясным, если принять во внима­ние, что при | С | > 1 величина СХ имеет возможные зна­чения (по абсолютной величине), большие, чем величина X. Отсюда следует, что эти значения рассеяны вокруг математического ожидания М (СХ} больше, чем возмож-

Свойство 3.

Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

D(X+Y)=D(X)+D(Y}.

Доказательство.

По формуле для вычисления дисперсии имеем

Раскрыв скобки и пользуясь свойствами математиче­ского ожидания суммы нескольких величин и произведе­ния двух независимых случайных величин, получим

Итак,

Следствие 1.

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Например, для трех слагаемых имеем

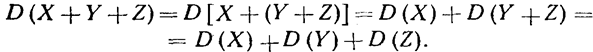
Для произвольного числа слагаемых доказательство проводится методом математической индукции.

Следствие 2.

Дисперсия суммы постоянной вели­чины и случайной равна дисперсии случайной величины:

Доказательство.

Величины С и Х независимы, поэтому, по третьему свойству,

В силу первого свойства D (С) == 0.

Следовательно,

Свойство становится понятным, если учесть, что ве­личины X и Х+С отличаются лишь началом отсчета и, значит, рассеяны вокруг своих математических ожиданий одинаково.

Свойство 4.

Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

Доказательство.

В силу третьего свойства

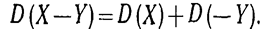
По второму свойству,

или

Дисперсия числа появлений события в независимых испытаниях (дисперсия биномиального закона распределения)

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна. Чему равна дисперсия числа появлений со­бытия в этих испытаниях? Ответ на этот вопрос дает следующая теорема.

Теорема. Дисперсия числа появлений события А в п не­зависимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления со­бытия в одном испытании:

Для оценки рассеяния возможных значений слу­чайной величины вокруг ее среднего значения кроме дис­персии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной ве­личины Х называют квадратный корень из дисперсии:

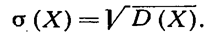
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному

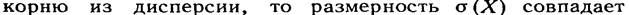
с размерностью X. Поэтому в тех случаях, когда жела­тельно, чтобы оценка рассеяния имела размерность слу­чайной величины, вычисляют среднее квадратическое от­клонение, а не дисперсию. Например, если Х выражается

Пример. Случайная величина Х задана законом распределения

Искомое среднее квадратическое отклонение

Дата добавления: 2014-01-07