Линйного программирования

ТРАНСПОРТНАЯ ЗАДАЧА

Основная задача линейного программирования

Различные практические задачи, сводящиеся к схеме линейного программирования, могут иметь линейные ограничения вида неравенств, другие – равенств, третьи как тех так и других.

Задача линейного программирования с ограничениями—равенствами носит название основной задачи линейного программирования (ОЗЛП).

Основная задача линейного программирования ставится следующим образом.

Имеется ряд переменных

x₁, x₂,......, x _n.

Требуется найти такие неотрицательные значения этих переменных, которые удовлетворяли бы системе линейных уравнений:

a₁₁ x ₁ + a₁₂ x ₂ +.... + a_1n x _n = b ₁;

a₂₁ x ₁ + a₂₂ x ₂ +.... + a_2n x _n = b ₂;

(2.1)

.......................... ….

a_m1 x ₁ + a_m2 x ₂ +.... + a_mn x _n = b _m,

и, кроме того, ОБРАЩАЛИ БЫ В МИНИМУМ линейную функцию

L = c₁ x₁ + c₂ x₂ + …….+ c_n x_n. (2.2)

Очевидно, случай, когда линейную функцию нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию

L^׳ = -- L = -- c₁ x₁ -- c₂ x₂ -- …….-- c_n x_n. (2.3)

Условимся называть д о п у с т и м ы м решение ОЗЛП любую совокупность переменных

x₁ ≥ 0, x₂ ≥ 0, ……, x _n ≥ 0,

удовлетворяющую уравнениям (2,1).

О п т и м а л ь н ы м решением будем называть то из допустимых решений, при которым линейная функция (2.2)

обращается в минимум.

ОЗЛП необязательно должна иметь решение. Может оказаться, что уравнения (2.1) противоречат друг другу; может оказаться, что они имеют решение, но не в области отрицательных значений x_1, x₂,....._, x _n.

Тогда ОЗЛП не имеет допустимых решений.. Наконец, может оказаться, что допустимые значения ОЗЛП существуют, НО СРЕДИ НИХ НЕТ ОПТИМАЛЬНОГО: ФУНКЦИЯ L в области допустимых решений неограниченна снизу.

Вопрос о существовании неотрицательных значений x_1, x₂,....._, x _n, удовлетворяющих системе уравнений (2.1) рассматривается в специальном разделе математики – линейной алгебре.

2.3 Геометрическая интерпретация основной задачи линейного программирования

Рассмотрим пример 1. Найти max (2 x₁ + 5 x₂) = z при условиях x₁ ≤ 400, x ₂ ≤ 300,

x₁ + x ₂ ≤ 500, x₁ ≥ 0, x ₂ ≥ 0.

Каждое из этих неравенств – ограничений определяет полуплоскости, пересечение которых дает многоугольник, который заштрихован на рис. 1. Этот многоугольник (выпуклый многогранник) и представляет собой допустимое множество решений К задачи линейного программирования.

\

Рассмотрим целевую функцию f (x₁, x₂) = 2 x₁ + 5 x₂.

Пусть f (x₁, x₂) = 1000 = z₁. График уравнения 2 x₁ + 5 x₂ = 1000 представляет собой прямую с отрезками на осях x₁ = 500 единиц, а x₂ = 200 единиц.

2 x₁ / 1000 + 5 x₂ / 1000 = x₁ / 500 + x₂ / 200 = 1.

При f (x₁, x₂) = 1500, получим прямую z₂, имеющую уравнение

2 x₁ / 1500 + 5 x₂ / 1500 = x₁ / 750 + x₂ / 300 = 1.

Прямая z₂ параллельна прямой z_1, но расположена выше ее. Двигая прямую вверх параллельно самой себе, приходим к положению z_max, когда прямая и множество К будут иметь только одну общую точку А. Очевидно, что точка А (x₁ = 200; x₂ = 300) оптимальное решение, так как она лежит на прямой с максимально возможным значением z_max. Заметим, что эта точка оказалась крайней точкой множества К.

Пример 2. Задача линейного программирования с семью переменными

x_1, x_2, x_3, x_4, x_5, x_6, x₇

имеет m = 5 уравнений – ограничений:

x₁ -- x₂ + x₃ = 4;

2 x₁ -- x₂ -- x₃ -- x₄ = --5; (2.4)

x₁ + x₂ -- x₅ = -- 4;

x₂ + x₆ = 5;

2 x₁ -- 2 x₂ -- x₆ + 2 x₇ = 7.

Требуется дать ее геометрическую интерпретацию и построить область допустимых решений ОДР, если она существует.

Решение. Выберем в качестве свободных переменных, например, x₁ и x₂ и выразим через них остальные (базисные) переменные: x_3, x_4, x_5, x_6, x_7. Из первого уравнения имеем:

x₃ = -- x₁ + x₂ + 4 (2.5)

Из третьего

х₅ = x₁ + x₂ + 4.

Из четвертого:

х₆ = -- x₂ + 5. (2.6)

Подставляя (2.5) во второе уравнение(2.3) и (2.6) -- в последнее и разрешая относительно x₄ , x₇, имеем:

х₄ = 3х₁ -- 2х₂ + 1;

х₇ = --х₁ + ½ х₂ + 6.

Геометрическая интерпретация задачи представлена на рис. 2 (прямые x₁ = 0, x₂ = 0 – оси координат; остальные ограничивающие прямые x₃ = 0, x₄ = 0, x₅ = 0, x₆ = 0,и x₇ = 0;

короткой штриховкой помечены допустимые полуплоскости -- условия неотрицательности переменных).

Как видно из расположения прямых и отмеченных полуплоскостей, допустимые решения для рассмотренной задачи существуют; они заполняют ОДР, которая на рис.2 показана закрашенной.

Далее найдем оптимальное решение ОЗЛП, обращающее в минимум линейную функцию семи неизвестных:

L = x₁ -- x₂ + 2x₃ -- x₄ -- 3x₅ + x₆ -- 2x₇ (2.7)

Выше были указаны условия-ограничения (2.4)., которые были разрешены относительно базисных переменных x_3, x_4, x_5, x_6, x₇, которые были выражены через свободные х₁ и х₂:

x₃ = -- x₁ + x₂ + 4

х₄ = 3х₁ -- 2х₂ + 1;

х₅ = x₁ + x₂ + 4. (2.8)

х₆ = -- x₂ + 5.

х₇ = --х₁ + ½ х₂ + 6.

Подставляя эти выражения в (2.7) и приводя подобные члены, имеем:

L = -- 5x₁ -- 2x₂ -- 12. (2.9)

Воспроизведем область допустимых решений, ранее построенную на рис. 2 (рис.3).

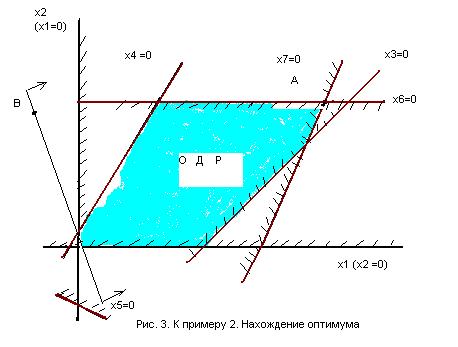
Отбрасывая свободный в (2.9), имеем:

L* = -- 5x₁ -- 2x_2.

Строим основную прямую L* = 0. Для этого откладываем отрезки γ₂ = -- 2 по оси абсцисс и -- γ₁ = 5 по оси ординат, проводим через точку В с координатами (--2, 5) прямую L* = 0 и отмечаем стрелками направление убывания L*. перемещая основную прямую параллельно самой себе в сторону убывания L*, наименьшее значение L* мы получим в точке А (наиболее удаленной от начала координат в направлении стрелок). Координаты этой точки х₁*, х₂* и дают оптимальное решение ОЗЛП. В точке А пересекаются две ограничивающие прямые: х₆ = 0 и х₇ = 0. Приравнивая нулю выражения для х₆ и х₇, получим два уравнения:

-- х₂ + 5 = 0

--х₁ + ½ х₂ + 6 = 0

Решая их совместно, найдем х₁* = 8,5; х₂* = 5.

Подставляя эти значения в (2.9), найдем оптимальные значения базисных переменных: х₃* = 0,5; х₄* = 16,5; х₅* = 17,5.

Что касается х₆ и х₇, то их оптимальные значения равны нулю: х₆* = 0;

Х₇* = 0.

Подставляя найденные оптимальные значения х₁* и х₂* в линейную функцию (2.9), найдем минимальное значение (оптимум) линейной функции L:

L = -- 5•8,5 -- 2• 5 -- 12 = --64,5.

Таким образом решаются задачи ОЗЛП в частном случае, когда m = n -- 2, при помощи геометрического построения.

2.4. Симплекс метод решения задачи

линейного программирования

Геометрическая интерпретация при решении задач линейного программирования перестает быть пригодной для этой цели при числе свободных переменных n –m > 3, а затруднительной уже при n –m = 3.

Для нахождения задачи линейного программирования в общем случае применяются не геометрические, а вычислительные методы. Из них наиболее универсальным является так называемый с и м п л е к с – м е т о д.

Пусть в задаче имеется n переменных и m независимых линейных ограничений, заданных в форме уравнений. Известно, что оптимальное решение (если оно существует) достигается в одной из опорных точек (вершин ОДР), где по крайней мере k = n -- m из переменных равны нулю. Выберем какие-то k переменных в качестве свободных и выразим через них остальные m базисных переменных. Пусть, например, в качестве свободных выбраны первые k = n -- m переменных х₁,х₂,..... х _k, а остальные через них:

x_k+1 = α _k+1,1 x ₁ + α _k+1,2 x ₂ +.....+ α _k+1,k x _k + β _k+1,

x_k+2 = α _k+2,1 x ₁ + α _k+2,2 x ₂ +.....+ α _k+2,k x _k + β _k+2, (2.10)

.................................................

x n = α _n,1 x ₁ + α _n,2 x ₂ +.....+ α _n,k x _k + β _n.

Попробуем, что будет, если положить все свободные переменные х₁,х₂,..... х _k равными нулю:

х₁ = 0, х₂ = 0,....., х _k = 0.

При этом получим:

x _k=1 = β _k+1, x _k=2 = β _k+2,...., x _n = β _n .

Это решение может быть допустимым или недопустимым. Оно допустимо, если все свободные члены неотрицательны. Предположим, что это условие выполнено. Тогда мы получили о п о р н о е р е ш е н и е. Но является ли оно оптимальным? Чтобы это проверить, выразим минимизируемую линейную функцию L через свободные переменные х₁,х₂,..... х _k:

L = γ₀ + γ₁ х ₁ + γ₂ х ₂ +.... + γ_k х _k. (2.11)

Очевидно, что при х₁ = х₂ =.....= х _k = 0 L = γ₀. Посмотрим, не можем ли мы улучшить решение, т.е. уменьшить функцию L, у в е л и ч и в а я какие-нибудь из переменных х₁,х₂,..... х _k (уменьшать мы их не можем, т.к. все они равны нулю, а отрицательные значения переменных недопустимы). Если все коэффициенты γ₁, γ_2,..... γ _k в выражении (2.11) п о л о ж и т е л ь н ы, то, увеличивая какие-то из переменных х₁,х₂,..... х _k сверх нуля, мы не можем уменьшить L; следовательно найденное нами опорное решение является о п т и -м а л ьн ы м. Если же среди коэффициентов γ₁, γ_2,..... γ _k в выражении (2.11) есть отрицательные, то, увеличивая некоторые из переменных х₁,х₂,..... х _k, а именно –те, коэффициенты при которых отрицательны, мы можем улучшить решение, т.е. уменьшить L.

Пример 3. Имеется задачалинейного программирования с ограничениями-неравенствами:

--5х₁ -- х₂ + 2х₃ ≤ 2,

--х₁ + х₃ + х₄ ≤ 5, (2.12)

--3х₁ + 5 х₂ ≤ 7.

Требуется минимизировать линейную функцию

L = 5х₁ -- 2х₃ .

Решение. Приводя неравенства к стандартному виду (≥ 0) и вводя добавочные переменные y₁, y₂, y₃, переходим к условиям-равенствам:

y₁ = 5х₁ + х₂ -- 2х₃ + 2,

у₂ = х₁ -- х₃ -- х₄ + 5_, (2.13)

у₃ = 3х₁ -- 5 х₂ + 7.

Число переменных n = 7 на 4 превышает число уравнений m = 3. Значит, четыре переменных могут быть выбраны в качестве свободных.

Попробуем выбрать в качестве свободных переменных х_1, х ₂, х _3, х₄ и положить их равными нулю. При этом получим опорное решение

х₁ = х ₂ = х ₃ = х₄ = 0; у₁ = 2; у₂ = 5; у₃ = 7.

При этих значениях переменных L = 0.

Посмотрим, является ли это решение оптимальным? Нет! Потому что в выражении линейной функции L коэффициент при х ₃ отрицателен. Значит, увеличивая х ₃ , можно уменьшить L.

Попробуем увеличивать х ₃ . Проследим по по уравнениям (2.13), опасно ли это для других переменных? Да, опасно для y₁ и у₂ -- в оба эти уравнения переменная х ₃ с отрицательным коэффициентом, значит, при увеличении х ₃ соответствующие переменные y₁ и у₂ могут стать отрицательными.

Посмотрим, какая из этих переменных y₁ или у₂ раньше обратится в нуль при увеличении х ₃ . Очевидно, y₁ ; она станет равной нулю при х ₃ = 1, а у₂ -- только при х ₃ = 5.

Поэтому выбираем переменную y₁ и вводим ее в число свободных вместо х ₃ . Чтобы «переразрешить» систему (2.13) относительно х ₃ , у₂ , у₃ , поступим следующим образом. Разрешим первое уравнение (2.13) относительно новой базисной переменной х ₃ :

х ₃ = _5/2 х₁ + ½ х₂ -- ½ y₁.

Это выражение вместо х ₃ подставим во второе уравнение; получим

у₂ = -- 3/2 х₁ -- ½ х₂ + ½ у₁ --х₄ + 4.

Что касается третьего уравнения, то оно, как не содержащее х ₃ , не изменится. Итак, мы привели систему (2.13) к виду:

х ₃ = _5/2 х₁ + ½ х₂ -- ½ y₁,

у ₂ = -- 3/2 х₁ -- ½ х₂ + ½ у₁ -- х₄ + 4, (2.14)

у₃ = 3х₁ -- 5 х₂ + 7

со свободными переменными х_1, х_2, у_1, х₄ и базисными х _3, у ₂, у_3.

Выразим линейную функцию L через новые свободные переменные:

L = 5х₁ -- 5х₁ -- х₂ + у₁ -- 2,

или

L = -- х₂ + у₁ -- 2. (2.15)

Положим теперь свободные переменные равными нулю. Линейная функция L станет равной –2. Это уже лучше, чем прежнее значение L = 0. Но является ли это решение оптимальным? Все еще нет, т.к. коэффициент при х₂ в выражении (2.15) отрицателен. Итак, будем увеличивать х₂. Посмотрим, для какой из переменных, стоящих в левых частях системы (2.14), это может быть «опасно». Только для у ₂ (в первое уравнение х₂ входит с положительным коэффициентом, а в третье совсем не входит).

Итак, обменяем местами переменные х₂ и у ₂ -- первую выведем из числа свободных, а вторую - введем. Для этого разрешим второе уравнение (2.14) относительно х₂ и подставим это х₂ в первое уравнение. Получим еще один вид системы (2.13):

х₃ = х₁ -- у ₂ -- х₄ + 5;

х₂ = -- 3х₁ -- 2у₂ + у₁ --2х₄ + 8; (2.16)

у₃ = 3х₁ -- 5 х₄ + 7.

Выразим L через новые свободные переменные:

L = 3х₁ + 2у₂ -- у₁ + 2 х₄ -- 8 + у₁ -- 2,

или

L = 3х₁ + 2у₂ + 2х₄ -- 10. (2.!?)

Полагая х₁ = у₁ = х₄ = 0, получим

L = -- 10.

Является ли это решение оптимальным? На этот раз - да, так как коэффициенты всех свободных переменных в выражении (2.17) неотрицательны.

Итак, оптимальное решение ОЗЛП найдено:

х₁* = 0, х₂* = 8, х₃* = 5, х₄* = 0, у₁* = 0, у₂ = 0; у₃ = 7.

При таких значениях переменных линейная функция принимает минимальное значение:

L_min = --10.

Заметим, что в рассмотренном примере нам не пришлось искать опорного решения: оно сразу же получилось, когда мы положили свободные переменные равными нулю. Это объясняется тем, что в уравнениях (2.13) все свободные члены были неотрицательны и, значит, первое же попавшееся оказалось опорным. Если это окажется не так, можно будет прийти к опорному решению с помощью такой же процедуры обмена местами некоторых базисных и опорных переменных, переразрешая уравнения до тех пор, пока свободные члены не станут отрицательными.

При решении практических задач обычно используется обычно используется табличный алгоритм замены базисных переменных. Процедура «переразрешения» системы уравнений-ограничений ОЗЛП при этом сводится к заполнению стандартных таблиц по определенной системе правил [ Л.6,7,8].

Симплекс-метод решения задачи линейного программирования является универсальным и применим для решения любых таких задач. Однако существуют некоторые частные типы задач линейного программирования, которые допускают решение более простыми методами. К ним, в частности, относится и транспортная задача.

Классическая транспортная задача ЛП формулируется следующим образом.

Имеется m пунктов отправления: А_1, А_2,...... : Аm_., в которых сосредоточены запасы какого-то однородного товара в количестве соответственно а₁, а₂, а_m, единиц. Имеется также n пунктов назначения:

В_1, В_2,........ В_m, подавших заявки соответственно на b₁, b₂,.....b_n, единиц товара.

Предполагается, что сумма всех заявок равна сумме всех запасов.

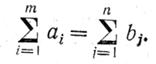(3.1)

Известна стоимость с _ij перевозки единицы товара от каждого пункта отправления Ai до каждого пункта назначения Bj. Таблица (матрица) стоимостей перевозки с _ij задана:

Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и при этом общая стоимость всех перевозок была минимальной.

Дадим этой задаче математическую формулировку. Обозначим x _{i j} - количество товара, направляемого из i-го пункта отправления Ai в j – й пункт назначения Bj (i = 1,..., m; j = 1,... n). Неотрицательные переменные х₁₁, х₁₂,...., х_mn (число которых, очевидно, равно (m × n) должны удовлетворять следующим условиям:

1. Суммарное количество товара, направляемое из каждого пункта отправления во все пункты назначения, должно быть равно запасу товара в данном пункте. Это дает нам m условий-равенств;

х₁₁ + х₁₂ +.... + х_{1 n} = а₁,

х₂₁ + х₂₂ +.... + х_{2 n} = а₂, (3,2)

........................

х m1 + х_m2 +.... + х_{m n} = а _m.

2. Суммарное количество товара, доставляемое в каждый пункт назначения изо во всех пунктов отправления, должно быть равно заявке, поданной каждым пунктом. Это даст n условий-равенств:

х₁₁ + х₂₁ +.... + х _m1 = b₁,

х₁₂ + х₂₂ +.... + х_m2 = b₂, (3.3)

........................

х _1n + х_2n +.... + х_{m n} = b_n.

3. Суммарная стоимость всех перевозок, т.е. сумма величин х _{i j} , умноженных на соответствующие стоимости с _{i j} должна быть минимальной:

L = c₁₁ x₁₁ + c₁₂ x₁₂ +.... + c_1n x_1n + c₂₁ x₂₁ + c₂₂ x₂₂ +....

c_2n x_2n +.... + c_m1 x _m1 + c_m2 x _m12 +.... + c_{m n} x _m n = min. (3.4)

Функция (3.4) линейна, ограниченная – равенства (3.2),(3.3) также линейны. Перед нами типичная задача с ограничениями – равенствами (ОЗЛП).

Как и всякую другую задачу линейного программирования, ее было бы решить симплекс-методом, но данная задача имеет некоторые особенности, позволяющие решить ее более просто. Причиной является то, что все коэффициенты при переменных в уравнениях (3.2),(3.3) равны единице. Кроме того имеет значение структура связи между условиями. Нетрудно убедиться, что не все m + n уравнений нашей задачи являются независимыми. Действительно, складывая между собой все уравнения (3.2) и все уравнения (3.3) мы должны получить одно и то же, в силу условия (3.1). Таким образом, условия (3.2), (3.3) связаны одной линейной зависимостью, и фактически из этих уравнений только m + n -- 1, а не m + n являются линейно независимыми. Значит, ранг системы уравнений (3.2),(3.3) равен

r = m + n --1

а, следовательно, можно разрешить эти уравнения

относительно m + n --1 базисных переменных, выразив их через остальные, свободные.

Подсчитаем количество свободных переменных. Оно равно:

k = mn -- (m + n –1) = mn -- m – (n –1) =

= m(n -- 1) – (n –1) = (m—1) (n –1).

Мы знаем, что в задаче линейного программирования оптимальное решение достигается в одной из вершин ОДР, где по крайней мере k переменных обращается в нуль. Значит в нашем случае для оптимального плана перевозок по крайней мере (m—1) (n –1) значений x _{i j} должны быть равны нулю.

Терминология. Независимо от того, что, транспортируется, откуда и куда (в условиях электроснабжения это может быть передача электроэнергии от электростанций потребителям)

значения x _{i j} количества единиц транспортируемого продукта, направляемых из пункта А_i

в пункт В_j мы будем называть п е р е в о з к а м и.

Любую совокупность значений (x _{i j} ) (i = 1,...., m; j = 1,... n), будем называть планом перевозок, или просто планом.

План (x _{i j} ) будет называться д о п у с т и м ы м, если он удовлетворяет условиям (3.2).(3.3)

(балансовым условиям)6 все заявки удовлетворены, все запасы исчерпаны.

Допустимый план будет о п о р н ы м, если в нем отличны от нуля не более r = m + n --1

базисных перевозок x _{i j,} а остальные равны нулю.

План (x _{i j} ) будем называть оптимальным, если он среди всех допустимых планов приводит к наименьшей стоимости всех перевозок.

Методы решения транспортной задачи сводятся к простым операциям непосредственно с таблицей, где в определенном порядке записаны все условия транспортной задачи. Такую таблицу называют т р а н с п о р т н о й т а б л и ц е й.

В транспортной таблице записываются

1) пункты отправления и назначения,

2) запасы, имеющиеся в пунктах отправления,

3) заявки, поданные пунктами назначения,

4) стоимости перевозок из каждого пункта отправления в каждый пункт назначения.

Стоимости перевозок помещают в правом верхнем углу каждой ячейки, с тем чтобы в самой ячейке при составлении плана помещать перевозки x _{i j} .

Образец заполнения транспортной таблицы

Таблица 3.1

пн по\	B1	B2		Bn	Запасы ai
А1	С11	С12		С1n	a1
А2	с21	с22		с2n	a2
………………	………………	………………………….	…………………………	…………………….
Аm	сm1	сm2		сmn	a m
Заявки	b1	b2		bn	∑ai = ∑bJ

Поскольку ранг системы уравнений-ограничений ТЗ равен r = n + m – 1, где

m – число строк, а n – число столбцов, следует утверждать, что в каждом опорном плане, включая и оптимальный, будут отличны от пуля не более чем r = n + m – 1 перевозок.

Ячейки (клетки) таблицы, в которых записываются отличные от нуля перевозки,

Называют базисными, а остальные (пустые) свободными.

Дата добавления: 2014-01-07