М е т о д о м п о т е н ц а л о в

Р е ш е н и е т р а н с п о р т н о й з а д а ч и

Распределительный метод решения ТЗ обладает одним недостатком: нужно отыскивать циклы для всех свободных клеток и находить их цены. Предлагаемый далее м е т о д п о т е н ц а л о в позволяет автоматически выделять циклы с отрицательной ценой и определять их цены.

Идея метода потенциалов сводится к следующему. Представим себе, что каждый из пунктов отправления А _i вносит за перевозку единицы товара какую-то сумму α _i; в свою очередь, каждый из пунктов назначения В_j также вносит за перевозку товара (все равно куда) сумму β _j ; Эти платежи передают ся некоторому третьему лицу «перевозчику».

Обозначим

α _i + β _j = с_{ί j} * (i = 1,..., m; j = 1,..., n)

и будем называть величину с_{ί j} * «псевдостоимостью» перевозки единицы товара из

А _i в В_j. Платежи не обязательно должны быть положительными.

Примем без доказательств следующие положения.

1. Суммарная псевдостоимость любого допустимого плана перевозок при заданных платежах (α _i, β _j ) одна и та жа и от плана к плану не меняется.

2. Если для всех базисных клеток плана (х_{i j} > 0)

α _i + β _j = с_{ί j} * = с_{ί j,}

а для всех свободных клеток (х_{i j} = 0)

α _i + β _j = с_{ί j} * ≤ с_{ί j,}

то план является оптимальным и никакими способами улучшен быть не может.

Можно показать, что эта теорема справедлива и для вырожденного плана, в котором некоторые из базисных переменных равны нулю.

Итак, признаком оптимальности плана (х_{i j}) является выполнение двух условий:

с_{ί j} * = с_{ί j} для всех базисных клеток; (3.5)

с_{ί j} * ≤ с_{ί j} для всех свободных клеток. (3.6)

План, обладающий таким свойством, называется п о т е н ц и а л ь н ы м, а соответствующие ему платежи (α _i, β _j ) -- п о т е н ц а л а м и пунктов А _i, В_j

(i = 1,..., m; j = 1,..., n).

Свойство платежей. При улучшении плана нам помогает следующее свойство платежей и псевдостоимостей:

Какова бы ни была система (α _i, β _j ), удовлетворяющая условию (3.5), для каждой свободной клетки цена цикла пересчета равна разности между стоимостью

с_{ί j} и псевдостоимостью с_{ί j} * в данной клетке:

γ _{i j} = с_{ί j} -- с_{ί j} *.

Пример. Решить методом потенциалов ТЗ, заданную в таблице 3.1, где имеется первый опорный план, составленный по способу северо-западного угла.

Таблица 3.10

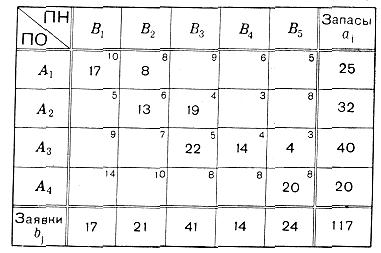
Решение. Приписываем к таблице3.10 снизу добавочную строку для платежей β _j, справа – добавочный столбец для платежей α _i (табл. 3.11).

Таблица 3.11

Псевдостоимости с_{ί j} * = α _i + β _j записываем в левом верхнем углу каждой клетки, а стоимости – в правом верхнем углу.

Один из платежей, например, α ₁, выбираем произвольно, полагая, скажем,

α ₁ = 0. Для каждой базисной клетки псевдостоимость с_{ί j} * = α _i + β _j должна быть равна стоимости с_{ί j}.

Итак, положим α ₁ = 0, находим из условия

α ₁ + β ₁ = 10; 0 + β ₁ = 10; β ₁ = 10,

а из условия

α ₁ + β ₂ = 0 + 8; β ₂ = 8.

Продолжая эту процедуру, находим:

α ₂ + β ₂ = α ₂ + 8 = 6; α ₂ = -- 2;

-- 2 + β ₃ = 4; β ₂ = 6;

α ₃ + 6 = 5; α ₃ = -- 1;

-- 1 + β ₄ = 4; β ₄ = 5;

--1 + β ₅ = 3, β ₅ = 4;

α ₄ + 4 = 8, α ₄ = 4.

Так как не все псевдостоимости в свободных клетках табл.3.11 удовлетворяют условию с_{ί j} * ≤ с_{ί j} , план, приведенный в табл, 3.11, не является оптимальным. Попробуем улучшить его, переводя в базисные одну из свободных клеток, для которых

с_{ί j} * > с_{ί j,} например, клетку (2,1). Строим соответствующий этой клетке цикл (показан в табл. 3.11). Цена этого цикла 5 -- 8 = -- 3.Перенесем по этому циклу 13 единиц товара (больше нельзя, чтобы перевозки в клетке (2,2) не стали отрица -- тельными), уменьшим стоимость плана на 13 • 3 = 39 и перейдем к таблице 3.12.

Таблица 3.12

Вычисляем для плана табл. 3.12 новые значения платежей, по-прежнему полагая

α ₁ = 0. Видим, что в табл. 3.12 все еще есть свободные клетки, для которых с_{ί j} * > с_{ί j,}

например, (1,4). Цикл этой клетки показан в табл. 3.12. Перенос четырех единиц по этому циклу приводит к плану, представленному (со своими платежами и псевдостоимостями) в таблице 3.13. Этот план все еще не оптимальный. Перенося по циклу, соответствующему свободной клетке (4,3), 20 единиц товара, получаем новый план (табл. 3.14) с новыми платежами и псевдостоимостями.

В табл. 3.14 уже все псевдостоимости не превосходят соответствующих стоимостей, значит, этот план о п т и м а л ь н ы й. Потенциалы пунктов найдениы и равны соответственно:

α ₁ = 0; α ₂ = --3; α ₃ = -- 2; α ₄ = 1;

β ₁ = 8; β ₂ = 8; β ₃ = 7; β ₄ = 6; β ₅ = 5.

Таблица 3.13

При анализе этих значений нельзя забывать, что одно из них (в нашем случае α ₁) назначено произвольно (α ₁= 0), поэтому потенциалы (или равносильные платежи) пунктов достаточно условны. Важно, что их сумма для всех перевозок, отличных от нуля, равна сумме стоимостей, проставленных в соответствующих клетках. Если смотреть на эти платежи не с точки зрения каждого пункта в отдельности, а с точки зрения всей совокупности пунктов (А,В), то безразлично, какой из пунктов платит больше, а какой – меньше.

Таблица 3.14

В случае, если план будет вырожденным, сценарий применения метода потенциалов будет аналогичным. Разница в том, что для получения первоначального опорного плана вводят ε – изменения запасов.

Мы рассмотрели только такую транспортную задачу, в которой сумма запасов равна сумме заявок. Однако существуют и другие типы ТЗ, например, ТЗ с неправильным балансом т др. Подходы к решению подобных задач широко описаны литературе, например, [Л 1,2 ].

Дата добавления: 2014-01-07