РГР № 1

Темы расчетно-графических работ

по математическим задачам электроэнергетике

Составить реферат по разделу «Применение методов теории вероятности в задачах электроэнергетики (12 – 15 с). В реферате обязательно отразить следующие вопросы:

1) понятие случайного события, случайной величины, случайного процесса. Примеры из области электроэнергетики.

2) определение математического ожидания, дисперсии, стандартного отклонения.

3) понятие о корреляции. Определение коэффициента корреляции.

4)понятие о математической статистике.

РГР № 2 Задача (Пример расчета смотри: Пример 1-18 стр 35)

В энергосистеме в течение шести суток наблюдались следующие мощности в 1000 МВт за характерные часы суток.

(4 12 16 19 24)

Часы суток	Мощность спроса за сутки в 1000 МВт
первые	вторые	третьи	четвертые	пятые	шестые
	а1	б1	в1	д1	е1	ж1
	а2	б2	в2	д2	е2	ж2
	а3	б3	в3	д3	е3	ж3
	а4	б4	в4	д4	е4	ж4
	а5	б5	в5	д5	е5	ж5

Рассматривая спрос как случайный процесс, 1. определить математические ожидания, дисперсии, стандартные отклонения и корреляционные коэффициенты для указанных сечений; 2. предсказать на основе этих данных спрос в 19 часов, если в 10 часов утра наблюдался спрос а2 МВт. Данные для расчета
№вар
а1
а2
а3
а4
а5
б1
б2
б3
б4
б5
в1
в2
в3
в4
в5
д1
д2
д3
д4
д5
е1
е2
е3
е4
е5
ж1
ж2
ж3
ж4
ж5

. Данные для расчета (продолжение)
№вар
а1
а2
а3
а4
а5
б1
б2
б3
б4
б5
в1
в2
в3
в4
в5
д1
д2
д3
д4
д5
е1
е2
е3
е4
е5
ж1
ж2
ж3
ж4
ж5

Пример расчета смотри: Пример 1-18 стр 35

РГР № 3 (См. стр 47-57)

Имеется m электростанций: А₁, А₂,.... А _m, которые могут вырабатывать электроэнергию в количестве соответственно а₁, а_2.,.... а _m МВТ.ч. Имеется n потребителей электроэнергии В₁, В₂,...., В n, подавших заявки соответственно на в_1, в_2,...., в _n МВТ.ч. Предполагается, что сумма всех заявок равна равна суммарной мощности всех электростанций.

Известна стоимость с _{i j} передачи электроэнергии от каждой электростанции A_i

до каждого потребителя В _j.Условия задачи заданы транспортной таблицей.

Требуется составить такой план передачи энергии от электростанций потребителям, чтобы все заявки были выполнены и при этом суммарная стоимость передачи энергии

была минимальна.

Вариант 1 Вариант 2

					a i
bj

					a i
bj

Вариант 3 Вариант 4

					a i
bj

					a i
bj

Вариант 5 Вариант 6

					a i
bj

					a i
bj

Вариант 7 Вариант 8

					a i
bj

					a i
bj

Вариант 9 Вариант 10

					a i
bj

					a i
bj

Вариант 11 Вариант 12

					a i
bj

					a i
bj

Вариант 13 Вариант 14

					a i
bj

					a i
bj

Вариант 15 Вариант 16

					a i
bj

					a i
bj

Вариант 17 Вариант 18

					a i
bj

					a i
bj

Вариант 19 Вариант 20

					a i
bj

					a i
bj

РАЗДЕЛ 3

МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ ИЗУЧЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С УЧЕТОМ НЕЛИНЕЙНОСТЕЙ

3-1. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНОГО процесса С ПОМОЩЬЮ ЧИСЛЕННЫХ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

При исследовании переходных процессов

в электрических системах необходимо решать системы обыкновен­ных дифференциальных уравнений. В большинстве случаев эти уравнения не линейны и их нельзя решить в общем виде. Иногда по условиям задачи может быть выбрана линейная модель, однако ее порядок высок, тогда более эффективными оказываются числен­ные методы решения. Отметим, что численное интегрирование — наиболее общий метод исследования переходных электромеханиче­ских процессов в электрических системах, особенно с учетом не­линейностей.

Прежде чем говорить о некоторых наиболее распространенных методах численного решения численного дифференциальных уравнений, рассмотрим первого порядка их общий подход на примере уравнения первого порядка

x^′ = f (t, x) (3-1)

Рассмотрение одного уравнения первого порядка не уменьшает общности получения результатов, так как все методы численного решения, применимые для уравнения (3-1). обобщаются для систем уравнений первого порядка, а уравнение n-го порядка можно свести к п уравнениям первого порядка. Пусть имеется уравнение второго порядка

x״ + ax′ = t².

Оно эквивалентно системе двух уравнений первого порядка:

x′ = y; y′ = t²– ay.

Как известно, общим решением уравнения (3-1) называется ре­шение, зависящее от произвольной постоянной интегрирования и содержащее все частные решения исходного уравнения. Очевидно, что подобное решение получить численными методами нельзя. Они используются для нахождения частного решения уравнения, удов­летворяющего заданным начальным условиям:

t = t_0, x(t₀) = x_0. (3-2)

Заменим в уравнении (3-1) производную х' отношением конеч­ных малых приращений Δх и Δt:

Δx/Δt=f{t, x),

откуда

Δ x = f{t, х)Δt (3-3)

Зная начальные условия интегрирования согласно (7-3), запи­шем приращение искомой функции на первом шаге в следующем виде:

Δx₁ = f (t₀ , x₀) Δt, т.е. x₁ = x₀ + Δx₁.

Аналогично получим приращения искомой функции на втором шаге, зная значение правой части уравнения (3-1) при t=t₁ и x = x₁

Отмечая нижним индексом «k-» значения переменных на k-м шаге интегрирования, представим (3-3) как

Δx_k+1 = f (t_k, x_k) Δt (3-4) или

Δx_{k + 1} = x_k + f (t_k, x _k) h (3-5)

где Δ t = h -- шаг интегрирования.

Рассмотрим геометрический смысл выражения (3-4),

зная, что

для производной—это тангенс угла наклона касательной L к интег­ральной кривой х (t) в заданной точке (t _k, x _k) по отношению к оси абсцисс (рис. 3-1). Метод численного решения дифференциального уравнения сводится к замене реальной интегральной кривой конеч­ным числом прямолинейных отрезков. При этом возникают ошибки двух видов: ошибка ограничения (локальная ошибка интегрирова­ния, показана на рис. 3-1 отрезком e) и накапливаемая (интеграль­ная) за время интегрирования ошибка. Наличие этих ошибок может приводить в некоторых случаях к совершенно неприемлемым результатам. Для их уменьшения есть только один путь—уменьшение шага интегрирования, что при неизменном полном времени

интегрирования ведет к удлинению счета. Таким образом, при не­обходимости получения более точного результата при том же шаге следует использовать другие, более точные методы интегрирования. Решение с помощью рядов Тейлора, Если функция х {t} в окрестности точки i достаточное число раз дифференцируема, то для нахождения ее значения при t+h можно воспользоваться разложени­ем Тейлора

n

Рис.3-1

Δx = x(t + h) – x(t) = ∑(x^(m)/ m!) h ^m + 0(hⁿ⁺¹), (3-6)

где все производные вычислены в исход- ной точке; O(h⁽ⁿ⁺¹⁾)означает, что в следующие члены ряда величина h входит в степени не ниже n+1,

т. е. ошибка ограничения в пер­вом приближении равна, Кhⁿ⁺¹, где K -- некоторая константа.

Данный метод теоретически пригоден для решения любых диф­ференциальных уравнений, однако при его практическом использо­вании встречаются довольно серьезные трудности. Они обусловлены тем, что при нахождении высших производных функций х в случае нелинейной правой части уравнения (7-1), выражения.для произ­водных все время усложняются по мере роста порядка производ­ной. Действительно, уже для второй производной имеем

x"=df(t, x)/dt+f{t, x)df(t, х)/дх.

Однако данный метод может служить эталоном при при сравнении с другими методами интегрирования поскольку все они в той или иной степени согласуются с разложением Тейлора. Так, например, метод, описанный выше и известный в литературе как метод Эйлера, является методом первого порядка, в котором выражение (3-5) согласуется с разложением Тейлора до членов с первой степенью h, т.е. в первом приближении ошибка ограничения этого метода равна Kh².

Таким образом, каждый метод интегрирования характеризуется порядком, хотя это не единственная характеристика метода. По­скольку все методы в той или иной степени согласуются с разло­жением Тейлора, то в методах, порядок которых выше единицы, высшие производные разложения (5-6) находятся косвенным обра­зом. При этом возможны два подхода. Первый—нахождение про­межуточных значений правой части уравнения (5-1) на интервале (t_k, t_k + h), а второй—использование значений функции х на пре­дыдущих шагах интегрирования. В случае метода п-го порядка при первом подходе необходимо n раз пересчитать правую часть уравнения (5-1), при втором—для определения x_k+1 дополнитель­ных пересчетов правой части уравнения делать не требуется и это обстоятельство является крайне благоприятным, так как умень-

шается продолжительность счета. Однако с помощью методов, по­рядок которых выше единицы, невозможно начать интегри­рование, поскольку они не содержат предшествующей информа­ции о ходе решения уравнения.

'Таким образом, все методы дополнительно можно классифици­ровать на одношаговые (самоиачинающие) и многошаго­вые, не дающие возможность начать решение.

Рассмотрим методы, наиболее широко используемые при ре­шении практических задач.

Методы Рунге — Кутта. Эти методы обладают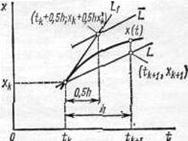

Рис. 3-2 Рис. 3-3

следующими свойствами:

1)являются одношаговыми;

2) согласуются с разложением Тейлора до членов порядка h^p, где p имеет различное значение для каждого метода и называется его порядком;

3) не требует вычисления производных от f(t, x).

можно трактовать как метод Рунге – Кутта первого порядка.

Причина значительных погрешностей метода Эйлера заключается в том, что для экстраполирования искомой функции на шаге интегрирования используется наклон касательной только в точке (t_k,x_k).

В методах Рунге—Кутта второго порядка для экстраполяции используется определенным образом усредненный наклон касатель­ных на шаге интегрирования. Методы Рунге—Кутта описываются формулой вида

x_k+1 = x_k + h Ф (t _k, x_k, h). (3-7)

Дата добавления: 2014-01-07