Теория погрешностей

Невозможно провести измерения с любой точностью (нулевой погрешностью). Существуют естественно – физические пределы точности измерений.

Это связано со следующими ограничениями:

а) квантовомеханическим принципом неопределенностей;

б) случайными флуктуациями измерительных устройств, называемых шумами.

Причины случайных флуктуаций:

· Броуновское движение.

· Шумы сопротивлений (тепловые шумы Джонсона). Всякое электрическое сопротивление R представляет источник случайных ЭДС, которые возникают в результате теплового движения электронов проводимости. Чтобы исключить случайные ЭДС, возникающие в металле, его нужно охладить до Т = 0, что невозможно.

· Шумы, обусловленные дискретностью вещества. Эти шумы связаны с тем, что, например, ток переносится отдельными электронами, или дырками (полупроводники).

· Помехи. Помехи могут возникать при скоплении статического электричества, при появлении паразитных колебаний напряжения в сети, внешним электромагнитным излучением и т.д.

Теория погрешностей справедлива только для случайных погрешностей.

Для оценки случайной погрешности физической величины Х необходимо проводить многократные измерения.

Мы начнем с наиболее простого случая, когда физическая величина Х измеряется n раз. Это означает, что процедуру измерения X надо проделать не менее n раз, причём обязательно в одних и тех же условиях.

Если бы никакие случайные факторы не влияли на результаты измерений, то, сколько бы раз не повторялась процедура измерения X, все результаты были бы совершенно идентичными.

Наличие случайных факторов приводит к тому, что серия (или выборка) из n измерений даёт n (объем выборки) разных значений величины X: (x₁, x₂,..., х_i, …, x_n). То, насколько велик разброс в этих n числах, и определяет случайную погрешность.

Частотное распределение измеренных значений можно представить с помощью диаграммы, которую называют гистограммой. Для этого область измеренных значений величины Х разбивают на некоторое количество интервалов (классов) одинаковой ширины Δх и определяют количество измерений n_i, попавших в каждый из этих интервалов (х_i ± Δх/2).

Гистограмма позволяет наглядно показать исход серии измерений. Хотя результат каждого измерения х_i определяется случайными причинами, из рис. 3.1 хорошо видно, что эта случайность подчиняется определенным законам.

Для описания серии измерений удобно вместо абсолютных частот n_i (n_i – количество результатов, попавших в класс х_i) ввести относительные частоты h_i = n_i/n (относительная частота появления результата х_i). Она нормирована на единицу: Σh_i = 1. При увеличении числа измерений n это распределение стремится к теоретическому распределению вероятностей, которое характеризует результаты бесконечного числа опытов.

Существование теоретического распределения вероятностей является основополагающим предположением теории погрешностей, которое, строго говоря, нельзя проверить экспериментально.

Математический предел при n → ∞ для каждого класса х_i выражается в виде

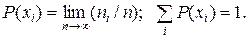(3.1)

Величина Р есть не что иное, как вероятность попадания измеряемого значения в интервал (i) при однократном измерении.

Теоретическое распределение вероятностей переходит при Δх → 0 в гладкую кривую. Вероятность попадания исхода одного измерения х в интервал Δх равна р(х)Δх. Функцию р(х) называют плотностью вероятности. В пределе при Δх → 0 плотность вероятности равна

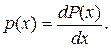(3.2)

Тогда вероятность Р попадания результата измерения в интервал [ x ₁, x ₂] равна

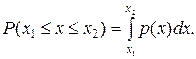(3.3)

Справедливо условие нормировки

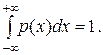(3.4)

Дата добавления: 2014-01-07