Правило 1

Правила расчета, округления и представления результата

В физике обычно имеют дело с приближенными числами, т.к. точные значения физических величин неизвестны. Данные числа получены с разной точностью и поэтому имеют разное количество значащих цифр. Следовательно, возникает естественный вопрос, что называют значащими цифрами и какие они бывают?

Значащими цифрами называются все цифры в десятичном изображении числа, кроме нулей, стоящих в начале числа.

Например, число 0, 0027030 содержит 5 нулей, три первых не являются значащими. Они устанавливают десятичный разряд остальных цифр. Нули после 7 и 3 являются значащими. Если число имеет большое количество нулей в начале или в конце числа, то его следует писать, используя степень.

0,0027030 = 2,7·10^-3 = 2,70·10^-3 = 2,703·10^-3 = 2,7030·10^-3 – правильно,

0,0027030 = 0,027·10^-1 = 0,270·10^-2 = 0,2703·10^-2 = 0,27030·10^-2 - не правильно.

Или

173000 = 1,73·10⁵ = 1,730·10⁵ – правильно,

173000 = 0,017·10⁷ = 0,173·10⁶ = 0,1730·10⁶ – не правильно.

Отсюда совет: никогда не надо загромождать число большим числом нулей спереди или сзади. В этом случае нужно придерживаться такого правила:

Результат измерения рекомендуется писать в виде х = а ·10ⁿ, где число а содержит перед запятой одну цифру, которая должна быть значащей. Число 10ⁿ следует вынести за скобки вправо (см. ниже).

В большинстве случаев, когда вопрос о точности измерений «остро» не стоит, приводят приближенную величину без указания ее погрешности. В этом случае, читатель или экспериментатор знают ее величину по принципу «умолчания».

Например: скорость тела задана как v₀ = 85 м/с, угол β = 35º, ускорение g = 9,8 м/с², то это значит, что Δ v ₀ = 1 м/с, Δ β = 1º, Δ g = 0,1 м/с².

Тогда истинное значение скорости находится в пределах:

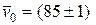м/с;

угла 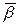= (35 ± 1)º;

ускорения 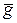= (9,8 ±0,1) м/с².

В примере со степенями:

2,7·10^-3 → (2,7 ± 0,1) ·10^-3;

2,70·10^-3 → (2,70 ± 0,01) ·10^-3;

2,703·10^-3 → (2,703 ± 0,001) ·10^-3, и т.д.

При использовании приближенных значений физических величин, без указания погрешности этой величины, следует пользоваться следующим правилом:

Правило 2.

В приближенном значении физической величины, все значащие цифры, кроме последней, нужно считать верными, а последняя цифра может отличаться от истинной на 1, но не более.[4]

Обычно при расчете приближенных физических величин используют калькулятор, не важно какой карманный или калькулятор персонального компьютера, которые высвечивают на табло от 8 до 32 цифр. Возникает вопрос – сколько их оставить?

Например:

.

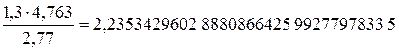Неправильное округление приводит к погрешностям, которые называются погрешностями вычислений, ничего общего не имеющие с погрешностями эксперимента. Наличие большого числа значащих цифр приводит к иллюзии, что результат получен с очень высокой точностью (10³¹), что недостижимо в современных экспериментах. [5]

Анализ приближенных чисел в примере показывает, что приближенное значение физической величины 1,3 получено с наименьшей точностью. Следовательно, погрешность этой величины на порядок и на два порядка превышает погрешность остальных величин. Из закона сложения погрешностей следует, что если погрешности отличаются в 3 и более раз, то меньшими погрешностями пренебрегают.

В данном примере результат должен быть записан так

.

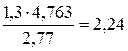Однако, при вычислении разных функций с разноточными значениями аргументов, применяют разные правила округления результата вычислений. (Привести примеры).

Существуют таблицы предельных абсолютных и относительных погрешностей вычислений для различного рода функций, которые можно найти в соответствующих книгах или в памяти РС.

Для нас в примере с округлением важно то, что мы округлили результат расчета до второй значащей цифры после запятой, хотя приближенная величина (с наименьшей точностью) известна до первой значащей цифры после запятой. Отсюда сформулируем следующее правило:

Правило 3.

Во всех вычислениях, промежуточные величины и их погрешности следует округлять на один, два порядка менее грубо.

Мы научились в приближенных физических величинах, представленных без погрешности, определять погрешность измерений и проводить с ними вычисления, сформулировав ряд правил.

Теперь сформулируем правила округления и записи результатов измерений в случае, когда мы сами рассчитываем абсолютную погрешность измерений.

Дата добавления: 2014-01-07