Правила округления и представления результата измерений с учетом абсолютной погрешности измерений

Как уже отмечалось выше, ни одну физическую величину невозможно измерить абсолютно точно. Поэтому, если, например, наш исследователь измерил плотность тела и сообщил Вам, что она равна 6,3×10³ кг/м³, то Вы можете быть уверены – это число несколько отличается от истинного значения плотности тела (исследователь и сам об этом знает). Если теперь ту же физическую величину (то есть плотность) измерит другой исследователь, то он может Вам назвать другое число – например, 6,27×10³ кг/м³. Но и это число тоже отличается от истинного значения.

С другой стороны, оба числа (6,3×10³ кг/м³ и 6,27×10³ кг/м³) - разные. Какое же из них ближе к истинному? Наверное, то, у которого больше цифр. Тот исследователь, который сообщил больше цифр, наверное, измерял точнее, следовательно, допустил меньшую погрешность.

Погрешность показывает, насколько тот, кто проводил измерения, гарантирует результат.

Как первый, так и второй исследователи, сообщив Вам свой результат, непременно сообщат и то, насколько они могли ошибиться. Сделают они это так.

· Первый исследователь: «плотность тела равна (6,3 ±0,1)×10³ кг/м³.

· Второй исследователь: «плотность тела равна (6,27 ±0,03)×10³ кг/м³.

Это значит, что первый исследователь гарантирует Вам, что значение плотности находится в интервале (6,2 ¸ 6,4)×10³ кг/м³, а его коллега гарантирует, что значение плотности находится в интервале (6,24 ¸ 6,30)×10³ кг/м³. Они не противоречат друг другу, и они оба правы. Однако второй исследователь провёл измерения точнее, допущенная им погрешность меньше.

Приведённый пример показывает, для чего нужно знать погрешность, если целью эксперимента является измерение некоторой физической величины. А если эксперимент ставится для проверки физической закономерности или закона? В необходимости знания погрешностей в этом случае мы убедимся в дальнейшем.

А вот студенты иногда дают ответы, например, такого типа: . Результат измерения содержит пять цифр, и это создаёт впечатление высокой точности измерения. Значение же абсолютной погрешности показывает, что студент, проводивший измерения, уверен только в первой цифре результата измерения 2, а во второй цифре 8 он сомневается (возможно, на самом деле 7 или 9). Но как он тогда может утверждать, что в третьей цифре он ошибается не более чем на 2? Ведь ошибка во второй цифре на единицу означает, что истинное значение измеряемого напряжения лежит в интервале . Это означает, что третья цифра в истинном значении напряжения может быть любой – от 0 до 9. То же самое относится, естественно, и ко всем остальным цифрам. Итак, правильно записать результат измерения надо так: . Несмотря на то, что здесь в результате измерения значительно меньше цифр, чем написал студент, ответ не стал менее точным. Студент же просто написал пять лишних (недостоверных) цифр – лишних потому, что ни в одной из них совершенно не уверен, ведь он сомневается уже во второй цифре результата измерения 8, поэтому цифры 3, 5 и 4 результата измерения и цифры 2 и 7 погрешности совершенно недостоверны.

Запомните это и никогда не пишите лишних цифр. А чтобы Вам легче было это запомнить, прочитайте внимательно следующее правило.

Правило 4.

При записи результата измерения абсолютную погрешность нужно округлять так, чтобы осталась только одна значащая цифра. После этого округляется результат измерения так, чтобы его последняя цифра находилась в том разряде, в котором находится единственная значащая цифра абсолютной погрешности.[6]

Здесь необходимо отметить следующее, что погрешность – это всегда потеря [7]. В измерениях - это потеря информации об измеряемой величине.

Поясним на примере. Пусть в ходе эксперимента измерено количество теплоты, полученное каким – то объектом, среднее значение которого равно

= 334, 4775 кДж.

Пусть абсолютная ошибка измерений составила,

в первом случае, 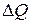= 0,0584 кДж.

Тогда результат измерений должен быть записан в виде

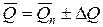= (334,48 ± 0,06) кДж = (334,48 ± 0,06)·10³ Дж.

Во втором случае 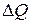= 0,584 кДж, тогда

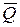= (334,5 ± 0,6) кДж.

В третьем случае 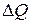= 5,84 кДж, тогда

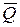= (334 ± 6) кДж.

В четвертом случае 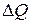= 58,4 кДж, тогда

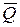= (330 ± 60) кДж = (33 ± 6)·10⁴ Дж.

В пятом случае 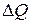= 584 кДж, тогда

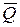= (300 ± 600) кДж =(3 ± 6)·10⁵ Дж.

Все! Информация об измеряемой величине потеряна. В этом случае необходимо применить измерительные приборы с более высокой точностью, и (или) изменить метод измерений.

Отсюда следует важный вывод: Чем выше точность измерений, тем больше значащих цифр в среднем значении измеряемой величины.

Дата добавления: 2014-01-07