Правила округления и представления результата измерений с учетом относительной погрешности измерений

Рассмотрим правила на примерах.

Примеры:

à Результат измерения тока: I = 1,818 А, расчётное значение абсолютной погрешности измерения: Δ(I) = 0,028 А. Относительная погрешность равна:

.

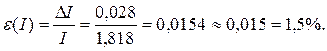
Обратите внимание на два факта в этом примере.

v Во-первых, при вычислении относительной погрешности использовались не окончательно округлённые значения абсолютной погрешности и результата измерения. Это сделано для того, чтобы на результат вычисления не повлияла вычислительная ошибка, то есть ошибка, связанная с процедурой вычисления (Правило 3). Повторим еще раз, правило здесь состоит в том, что во все формулы, по которым производятся какие-либо вычисления, нужно подставлять или точные числа, или приближенные числа, округлённые на один-два порядка менее грубо, чем это необходимо для записи окончательного результата. В данном примере в запись окончательного результата войдут числа: I = 1,82 А, Δ(I) = 0,03 А, поэтому при вычислении относительной погрешности использовались значения тока и абсолютной погрешности, округлённые менее грубо – в них было оставлено дополнительно по одной значащей цифре справа.

v Во-вторых, после вычисления относительной погрешности полученное число округлено. Казалось бы, оно должно быть округлено по тому же правилу, по которому округляется абсолютная погрешность, то есть до одной значащей цифры, но мы видим число e(I) = 0,015 = 1,5%, в котором две значащих цифры. Причина этого в том, что в записи относительной погрешности допускается оставлять одну или две значащие цифры. Если при округлении относительной погрешности до одной значащей цифры эта цифра оказывается равной 1, 2 или 3, а следующая за ней цифра (отброшенная) близка к 5, то округлить число надо до двух значащих цифр, причём вторую цифру надо заменить на 5. Например, число 6,62% надо округлить до 7%, а число 23,1% – можно до 20%, но лучше – до 25%. В нашем примере число 0,154 = 1,54% можно округлить до 2%, но лучше – до 1,5%.

При записи результата измерения следует дополнять его как абсолютной, так и относительной погрешностью. Рекомендуется это делать так:

à Пример 1.

à Пример 2.

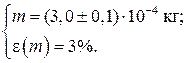
à Пример 3.

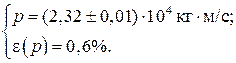
Дата добавления: 2014-01-07