Двумерные преобразования

Геометрические преобразования

Рассмотрим преобразования координат точек на плоскости. На рисунке 5 точка A перенесена в точку B.

Рис. 5. Операция переноса точки A в точку B.

Математически этот перенос можно описать с помощью вектора переноса 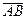. Пусть радиус вектор, соответствующий вектору переноса 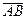. Тогда переход из точки A в точку B будет соответствовать векторной записи . Отсюда получаем, что для переноса точки в новое положение необходимо добавить к ее координатам некоторые числа, которые представляют собой координаты вектора переноса:

(1)

Масштабированием объектов называется растяжение объектов вдоль соответствующих осей координат относительно начала координат. Эта операция применяется к каждой точке объекта, поэтому можно также говорить о масштабировании точки. При этом, конечно, речь не идет об изменении размеров самой точки. Масштабирование достигается умножением координат точек на некоторые константы. В том случае, когда эти константы равны между собой, масштабирование называется однородным.

Рис. 6. Операция масштабирования.

На рис.6 приведен пример однородного масштабирования треугольника ABC. После применения операции однородного масштабирования с коэффициентом 2 он переходит в треугольник A^'B^'C^'. Обозначим матрицу масштабирования

. (2)

Для точек A и A^' операция масштабирования в матричном виде будет выглядеть следующим образом:

. (3)

Или в матричном виде

A^' = A S (4)

Рассмотрим далее операцию вращения точки на некоторый угол относительно начала координат. На рисунке 7 точка A = (x, y) переходит в точку B = (x^', y^') поворотом на угол a.

Рис. 7. Операция поворота точки A на угол a.

Найдем преобразование координат точки А в точку В. Обозначим b угол, который составляет радиус-вектор 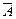с осью Оx. Пусть r – длина радиус-вектора 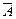, тогда

(5)

Так как 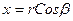и , то подставляя эти выражения в уравнения для x ^' и y ^', получаем:

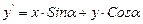(6)

В матричном виде вращение точки А на угол a выглядит следующим образом:

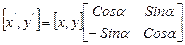(7)

Введем обозначение

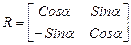
Тогда в матричном виде получим

A^' = A R (8)

Дата добавления: 2014-01-07