Трехмерные матричные преобразования

Подобно тому, как двумерные преобразования описываются матрицами размером 3´3, трехмерные преобразования могут быть представлены матрицами размером 4´4. Тогда трехмерная точка (x, y, z) записывается в однородных координатах как (Wx,Wy,Wz,W), где W ¹ 0. Для получения декартовых координат надо первые три однородные координаты разделить на W. Два однородных вектора описывают одну декартову точку в трехмерном пространстве, если H₁ = c H₂, где c = const ¹ 0 и H, H₂ - векторы, записанные в однородных координатах.

Матрицы преобразований будем записывать в правосторонней системе координат (см. рис. 10).

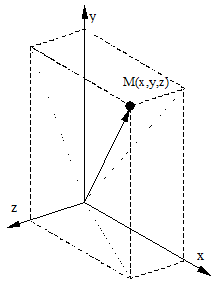
Рис. 10. Правосторонняя система координат

При этом положительный поворот определяется следующим образом. Если смотреть из положительной части оси вращения (например, оси 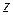) в направлении начала координат, то поворот на 90⁰ против часовой стрелки будет переводить одну положительную полуось в другую (ось x в y, y в z, z в x в соответствии с правилом циклической перестановки).

Заметим, что на практике во многих приложениях компьютерной графики удобнее применять левостороннюю экранную систему координат (см. рис. 11), в которой ось x направлена вправо, ось y – вверх, а ось z вглубь экрана. В этом случае удобнее интерпретировать тот факт, что точки с большими значениями 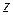находятся дальше от наблюдателя.

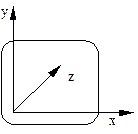
Рис. 11. Левосторонняя система координат

Запишем теперь матрицу трехмерного переноса, по аналогии с двумерным случаем:

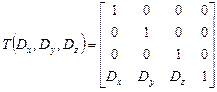, (13)

при этом

.

Операция масштабирования:

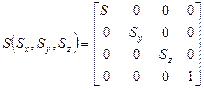, (14)

Перейдем к операции поворота. C ней в трехмерном случае придется разбираться чуть больше, чем в двумерном. Так как при двумерном повороте в плоскости xy координаты z остаются неизменными, то поворот вокруг оси z записывается так:

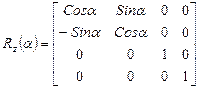. (15)

Матрицы поворота вокруг оси x и вокруг оси y имеют вид:

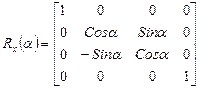,. (16)

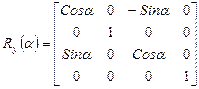:. (17)

Обратите внимание на смену положения синуса угла с отрицательным знаком в матрице поворота вокруг оси y. Правильность этих матриц легко проверить поворотом одного из ортов на 90⁰, при этом он должен перейти в следующий по порядку орт на соответствующей координатной оси.

Обратные преобразования будут выражаться матрицами, обратными к показанным выше. Для операции переноса надо лишь заменить знаки компонент вектора переноса на противоположные:

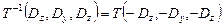;. (18)

для операции масштабирования – на обратные значения:

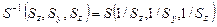;. (19)

для поворота – выбором отрицательного угла поворота:

.. (20)

Результатом нескольких последовательных поворотов будет матрица вида

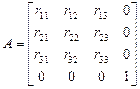. (21).

Здесь верхняя матрица размером 3´3 называется ортогональной. Столбцы ортогональной матрицы – это единичные вектора, в которые преобразуются орты координатных осей в результате поворотов. Важным ее свойством является то, что обратная к ней матрица является транспонированной: 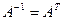. Это полезно тем, что при вычислениях достаточно поменять индексы местами и обратное преобразование получается автоматически.

После перемножения любого числа матриц вида T,S и R результирующая матрица всегда будет иметь вид:

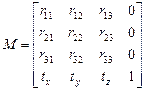. (22)

Здесь верхняя часть размером 3´3 определяет суммарный поворот и масштабирование, а три коэффициента последней строки – суммарный перенос.

Преобразование одной точки выполняется с помощью следующих действий

(23)

Таким образом, для преобразования одной трехмерной точки потребуется уже 9 умножений и 9 сложений.

Дата добавления: 2014-01-07