Предельное равновесие полигональных пластин

При определении разрушающей нагрузки, действующей на пластину, теория предельного равновесия (кинематический метод) позволяет решать задачу, оставаясь в пределах одномерной общей теории пластичности.

Пусть на пластину, представляющую собой в плане многоугольник, действует сосредоточенная сила, приложенная в точке С (рис. 2.3). Экспериментально показано, что несущая способность пластины исчерпывается тогда, когда по линиям вероятного разрушения, соединяющим точку С с углами «» пластины будут действовать погонные изгибающие моменты:

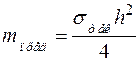. (2.5)

где 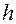- толщина пластины.

При этом зависимость (2.2) представляется в виде (2.6 – 2.7) при распределенной и сосредоточенной нагрузке.

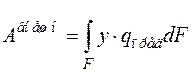. (2.6)

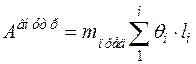. (2.7)

Здесь 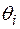- двугранный угол, образуемый по линии вероятного разрушения, 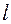- длина этой линии вдоль, которой действует m_пред.

На рис. 2.3 представлена пятиугольная пластина, шарнирно опертая по контуру и нагруженная силой 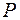в точке С. Линии, соединяющие точку приложения силы с углами пластины соответствуют минимальному значению работы внутренних сил при разрушении.

Для определения величины двугранного угла 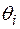проведем линию 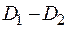, перпендикулярную . Максимум прогибов в момент разрушения обозначим «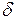». Очевидные преобразования с использованием приведенной схемы позволяют определить :

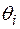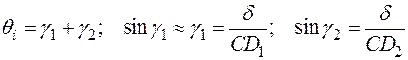
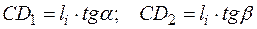
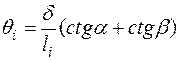. (2.8)

Рис.2.3

Подстановкой (2.8), (2.6) в (2.2), получим:

,

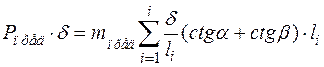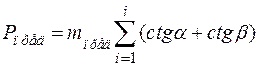. (2.9)

Рассмотрим несколько примеров.

1. Квадратная плита шарнирно оперта по контуру и нагружена сосредоточенной силой 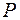в центре. Линии разрушения соединяют точку приложения силы с углами плиты (рис. 2.4). , ,

.

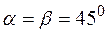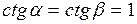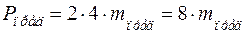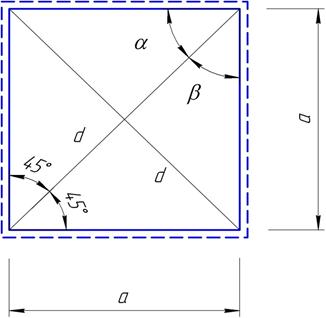
Рис.2.4

2. Правильный многоугольник. Опирание шарнирное.

Сила приложена в центре (рис. 2.5).

, ,

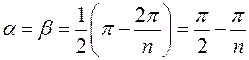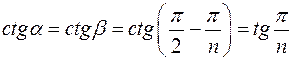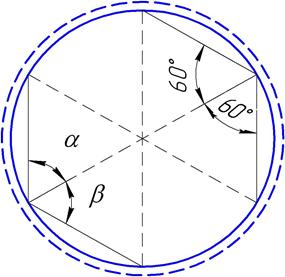
Рис.2.5

.

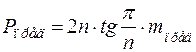3. Шарнирно опертая плита круглого очертания в плане с силой, приложенной в центре.

Положим в предыдущем решении 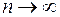, тогда:

,

.

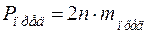4. Квадратная плита со стороной 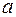, шарнирно опертая и нагруженная равномерно распределенной нагрузкой .

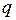. (2.10)

Здесь - объем пирамиды разрушения одинаков при действии распределенной нагрузки и сосредоточенной силы .

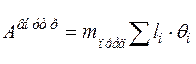, (2.11)

,

.

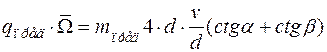5. Квадратная плита под действием равномерно распределенной нагрузки. Плита, шарнирно опертая по трем сторонам и заделанная по одной стороне.

Рис.2.6

Работа внешних сил такова же, как и в предыдущем случае:

.

Работа внутренних сил такова аналогична предыдущему случаю, но и имеет место цилиндрический шарнир в заделке:

.

Первое слагаемое в скобках соответствует выражению (2.11), второе – работа внутренних сил в заделке:

,

.

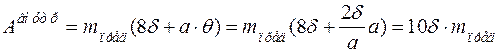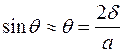
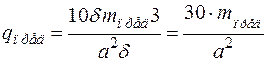
Дата добавления: 2014-01-07