Нахождение функциональных связей

Теоретические обобщения

Закономерности развития явлений

Вторым этапом исследования является обобщение экспериментальных данных. Наблюдения обобщают не только по окончании опытов, но и в процессе их получения. Исследователь всегда стремиться, еще в процессе опытов, установить закономерности, возможные отклонения и их причины, новые факторы, связи и взаимодействия. Для обобщения используют все материалы наблюдений: результаты измерений, описание развития явлений, фотографии, образцы, спектрограммы и так далее. Сопоставляя все материалы исследования, исследователь ищет раскрытие связей, взаимодействия, функциональных зависимостей факторов. Установив их, он выделяет главные связи, зависимости и устанавливает общие закономерности явлений. При обработке опытных данных необходимо стремиться как можно более разносторонней представить различные связи не ограничиваясь нахождением средних величин; сопоставлять значения отклонений, скорости изменения величин и соответствующих ускорений, максимумов и минимумов; проверять колебания на возможность гармонического анализа или устанавливать показатель их затухания; сравнивать различные величины, расположенные в порядке увеличения или уменьшения их значений и применять другие приемы.

Как простые, так и более сложные связи желательно выражать математически, чтобы формулы отображали закономерности физических процессов. Если исследователь не устанавливает причин, обусловливающих закономерность, то она всегда носит характер некоторой вероятности, а не достоверности. Закономерность достоверна лишь в том случае, если она вытекает из физической сущности наблюдаемых явлений.

Экспериментальные данные обобщают в такой последовательности: находят функциональные связи, устанавливают основные закономерности, раскрывают их физическую сущность, математически выражают их, а затем теоретически обобщают и развивают. К обобщению следует привлекать и материалы других исследований, из которых по каким либо причинам не сделаны должные выводы.

Методы математической обработки опытных данных разработаны довольно широко и изложены в ряде специальных работ. Исследователь должен ясно представлять, что современный математический аппарат – это могучий аппарат глубокого познания объективных законов природы.

Функциональные связи легче найти, если данные опытов представить таблицами и/или графиками. В таблице вначале выделяют по физическому смыслу аргумент (независимую переменную), затем функцию (зависимую переменную).

Пример. Пусть при измерении оборотов коленчатого вала двигателя в лабораторный журнал синхронные данные записаны в следующем виде:

Данные опытов без выделения аргумента
1 Сопротивление трения, кг	6,70	5,85	8,0	5,50	6,10	7,50
2 t воды в системе охлаждения
3 t масла в картере
4 обороты коленчатого вала в минуту

В таком виде данные опытов трудно читать и закономерности остаются неясными. Выделим по физическому смыслу аргумент. Понятно, что t воды и масла не может быть аргументом, потому что они изменяются не значительно. Сопротивления трения не регулировали и интервалы по нему между данными различных опытов не равномерны. Из этих соображений считаем аргументом число оборотов вала двигателя в минуту и расположим аргумент в возрастающем порядке. За аргументом расположен как наиболее существенную функцию данных о сопротивлению трения.

Число оборотов вала в минутах	Сопротивления трения	t воды	t масла
	5,50
	5,85
	6,10
	6,70
	7,50
	8,00

Как видно из таблицы функциональные связи стали гораздо яснее. Общей закономерностью является увеличение сопротивления трения и понижения температуры воды в системе охлаждения в функции числа оборотов вала. Температура масла немного изменяется лишь при максимальных оборотах.

Сложнее составить таблицу при большой повторности измерения. В таких случаях лучше использовать свойство вариационных радов, когда объединяют только качественно однородные величины. Предположим, что произведено 36 замеров секундного расхода воды получим следующие замеры в литрах

1,8	6,6	11,3	13,0	16,6	15,1	17,0	15,0	32,7
24,7	20,7	14,5	3,6	6,9	21,2	15,8	1,9	7,7
21,8	14,1	25,1	25,2	12,7	15,2	25,4	8,8	21,5
17,2	5,3	23,0	13,3	16,3	9,7	21,8	17,9	13,5

Общая сумма опытных значений составляет = 553,9л за 36 сек.

Для вычисления дисперсии и стандарты берем разницы а_i, и их квадраты. Покажем вычисления для первых трех разностей:

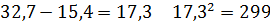
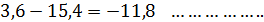
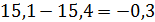
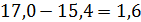
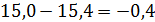
Общая сумма квадратов 36 конкретных величин от средней будет равна

Существенным признаком вариационного ряда является разделение всех полученных при измерении величин на группы или классы. Желательно, чтобы классовые промежутки (интервалы) были равномерными (с постоянным шагом), так как это значительно облегчает обработку табличных данных. Каждый класс характеризуется двумя признаками: пределами, в которых заключаются входящие в класс величины и количеством n_i измерений входящих в данный класс. Это количество называется частотой. Пределы классов не должны перекрывать один другого. Слишком узкие пределы (дробная разбивка на мелкие классы) усложняют вычисления и затеняют общие закономерности распределения случаев измерения, но увеличивает точность вычислений. В пределе приближаясь к точности вычислений по всем измерениям в совокупности. Слишком широкие пределы яснее показывают закон распределения, но увеличивает ошибку вычислений, делают их менее близкими к конкретным данным опытам. Таким образом, если исследователя интересует закономерность распределения случаев, то количество классов, на которые разбивают все данные измерений, должно быть уменьшено. А широта пределов каждого класса (классовые интервалы) увеличено. И наоборот.

Практика показывает, что количество классов не следует делать менее 5 и более 12. И что в пределах данного класса должно находиться несколько измерений. В отдельных случаях количество классов может быть больше 12. Рекомендуется предварительную зависимость количества классов от общего количества измерений.

Количество измерений 10-30 31-70 >70

Количество классов 5 6-9 10-12

Данные опытов разбивают на классы таким образом: берут крайние значения измеренной величины округляют в большую или меньшую сторону и делят на количество классов. Результат (классовый интервал) определяют так, чтобы средний по классу была не слишком дробной величиной.

Дата добавления: 2014-01-07