Уфа 2007

АЛГОРИТМЫ

ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ

КУРС ЛЕКЦИЙ

Автор: доцент кафедры ВТИК УГНТУ Мухамадеев И.Г.

Текст подготовил: ст. гр. ТЭ-03
Валишин А.Р.

Литература по вычислительной математике

Основная литература:

1. Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высшая школа, 1990.

2. Демидович Б.П., Марон Н.А. Основы вычислительной математики. - М.: Наука, 1970. – 660 с.

3. Гловацкая А.П. Методы и алгоритмы вычислительной математики. - М.: Радио и связь, 1999. - 408 с.

4. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. – М.: Финансы и статистика, 1999.

5. Потёмкин В.Г. Система MATLAB. Спр. пособие. – М.: Диалог - МИФИ. 1998 – 350 с.

6. Умергалин Т.Г. Основы вычислительной математики: Учебное Пособие. - Уфа, Изд-во УГНТУ, 2003. – 106 с.

7. Джонсон К. Численные методы в химии. – М.: Мир,1983. – 504 с.

8. Шуп Т.Е. Прикладные численные методы в физике и технике. - М:. Высш. Шк., 1990.

9. Очков В.Ф. MathCAD 7.0 Pro для студентов и инженеров. М:. Компьютер-Пресс, 1998. = 384 с.

10. Дьяконов В.П. Справочник по применению системы EUREKA.-М.: Физматлит, 1993.-96 с.

Учебные пособия:

1. Мухамадеев И.Г. Решение систем нелинейных уравнений. /Мет. указания/. – УНИ, Уфа. – 1988 г. (7 / 11)

2. Кирлан Л.Д. Приближенные методы решения дифференциальных уравнений и их систем на мини- и микро-ЭВМ. /Мет. указания/. – УНИ, Уфа. -1987 г.

3. Калиновский Ю.В., Мухамадеев И.Г. Решение алгебраических и трансцендентных уравнений. /Мет. указания/. – УНИ, Уфа – 1987 г.
(7 / 6).

4. Калиновский Ю. Кайбышева Д.А. Мухамадеев И.Г. Численное интегрирование /Мет. указания/. – УНИ, Уфа, 1988

5. Иванов В.И., Лизунов А.Н., Мухамадеев И.Г.Аппроксимация функций /Мет. указания/. - Уфа, Изд. Уфим. нефт. института, 1989.

Тема 1

Введение.

В настоящее время в науке и инженерной практике широко используется метод математического моделирования.

Математическим моделированием [1] называется изучение реального объекта на ЭВМ с помощью математической модели этого объекта.

Например:

1. Совершенствование ядерного оружия путем расчетов на супер-ЭВМ. Удалось отказаться от испытаний ядерного вооружения.

2. Компьютерные тренажеры (симуляторы), созданные на основе математических моделей, появились сначала у военных, сейчас они широко применяются в производственном и учебном процессе.

Математическая модель – это приближенное математическое описание объекта (технологического процесса, реакции, явления и т.д.).

Примеры простейших моделей:

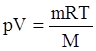уравнение состояния идеального газа (1.1)

F = закон всемирного тяготения (1.2)

закон сохранения энергии (1.3)

закон Кулона (1.4)

закон сохранения энергии для фотона, (1.5)
где v – частота излучения.

Сложные модели описывают объект точнее (адекватнее [2] ).

Математическое моделирование позволило исследовать на ЭВМ очень сложные процессы, такие, например, как глобальные климатические изменения в результате применения ядерного оружия (натурный эксперимент имеет катастрофические последствия).

В литературе математическое моделирование часто принято называть вычислительным экспериментом.

Основные этапы математического моделирования:

1. Разработка модели – формализация. Изучается в прикладных и фундаментальных науках.

2. Разработка метода (алгоритма) решения уравнения модели – алгоритмизация. Изучается в вычислительной математике.

3. Создание программы – программирование. Изучается в информатике.

4. Расчеты, анализ результатов – практическое использование.

	Использование результатов:

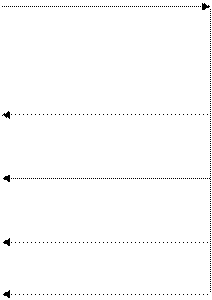
Результат

	Расчёты

Программа

для совершенствования

Алгоритм

		алгоритма

для совершенствования

Мат. модель

проектирования

Объект

Предметом вычислительной математики являются численные методы (алгоритмы) решения математических задач, возникающих при исследовании реальных объектов методом математического моделирования.

Например, пусть нужно найти R из уравнения (1.2) или (1.4), из уравнения (1.3) или c из уравнения (1.5). Что общего в этих задачах? То, что нужно решить уравнение вида:

x ² = a (1.6)

Вычислительная математика не рассматривает решения конкретных задач (1.2÷1.5), а изучает их решение в общем, абстрактном виде (1.6).

С точки зрения обычной математики точное решение уравнения (1.6) имеет вид:

= ,

причем если a > 0, то два вещественных решения;

если а = 0, то тривиальное решение ;

если а < 0, то вещественных решений нет.

Но знак 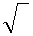не решает задачу, так как не дает практического способа (алгоритма) вычисления значения х для конкретного значения а.

Вычислительная математика предлагает следующий алгоритм вычисления x*:

1. Выбрать начальное значение х, например 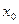=а. Это начальное приближение решения.

2. Вычислять новые приближения решения x_i по формуле:

x_i = (1.7)

до достижения условия:

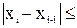e (1.8)

Здесь i = 1,2,.. – номер вычисления - итерации.

e – требуемая точность.

Пример. Нужно решить уравнение 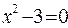с точностью e=0,001.

Зададимся ,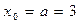

Вычислим первое приближение: ,

оценим точность | x₁ – x₀ | = 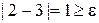.Требуемая точность не достигнута, нужно продолжить расчет.

Вычислим второе приближение: ,

оценим точность .

Вычислим третье приближение: ,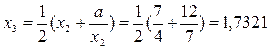

оценим точность .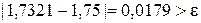

Вычислим четвертое приближение: ,

оценим точность − точность достигнута.

Ответ: .

Точное значение (до 8 значащих цифр):

Рассмотренный пример демонстрирует принципы, общие для итерационных методов решения задач вычислительной математики:

1. Исходная задача (1.6) заменяется другой задачей – вычислительным алгоритмом по формулам (1.7), (1.8), где используются только арифметические операции +. Принято называть (1.7) формулой итерационного процесса (итерационным процессом), (1.8) - условием завершения итерационного процесса.

2. Задача (1.7) содержит новый параметр i – номер итерации. Очевидно, что число итераций влияет на точность решения.
Если , то итерационный процесс является сходящимся – позволяет получить решение исходной задачи (1.6).

3. Решение, полученное итерационным методом, всегда является приближенным, так как точное решение получить невозможно – нужны бесконечные вычисления.

Важно подчеркнуть, что формула (1.7) получена из (1.6) путём тождественных преобразований:

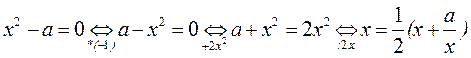
Но не всякое тождественное преобразование позволяет получить сходящийся итерационный процесс.

Например:

a)

Выполним расчет при а=3:

; ; ;

Итерационный процесс не сходится; значения приближений колеблются.

б)

; …

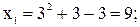
Итерационный процесс расходится.

Рассмотренный пример иллюстрирует один из видов численных методов – итерационный.

Виды численных методов:

1. Прямые – решение получают за конечное число арифметических действий.

2. Итерационные – точное решение может быть получено теоретически в виде предела бесконечной сходящейся последовательности вычислений.

3. Вероятностные – методы случайного поиска решения (угадывания).

Все виды численных методов позволяют получить только приближенное решение задачи, то есть численное решение всегда содержит погрешность.

Тема 2

Структура погрешности численного решения задачи.

Точность решения задачи оценивается абсолютной или относительной погрешностью.

Абсолютная погрешность:

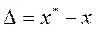, (2.1)

где - точное решение,

x - численное решение.

Относительная погрешность:

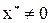, (2.2)

Источники погрешности численного решения задачи:

1. Погрешность математической модели.

Возникает в результате допущений, принятых при получении модели. Реальность всегда сложнее любой модели, поэтому этот источник погрешности всегда влияет на численное решение. Величина этой погрешности определяется сравнением экспериментальных данных с результатами расчетов по модели (оценивается адекватность модели объекту).

2. Погрешность исходных данных.
Зависит от точности измерения параметров, используемых в модели. Любые измерения приближенны, поэтому и этот источник всегда влияет на решение.

В вычислительной математике эти два вида погрешности (погрешность математической модели и погрешность исходных данных) принято называть неустранимой погрешностью, т.к. она не зависит от метода решения задачи и всегда влияет на ее решение, и ее обязательно нужно учитывать при анализе полученного решения.

3. Погрешность метода решения задачи.
Возникает в результате применения итерационного или вероятностного метода решения.
Эти методы позволяют получить точное решение только в результате бесконечной последовательности действий. Поэтому для получения приближенного решения бесконечный процесс прерывают при достижении требуемой точности решения.

4. Погрешность округления .
Возникает в результате проведения вычислений с конечным числом значащих цифр.

Погрешность элементарных арифметических действий изучается в теории погрешности. Учесть погрешность округления при большом количестве арифметических действий практически невозможно.

Есть случайные и систематические источники погрешности округления.

Случайные источники обычно компенсируют друг друга.

Например:

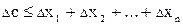
Знаки случайны и компенсируют друг друга при большом n.

Систематические источники вызывают накопление погрешности округления. Они являются дефектом структуры вычислений (алгоритма).

Пример 2.1

Требуется вычислить:

Сложим эти числа столбиком и, округлив результат до 3-х значащих цифр, получим значение с:

0,476

0,411

1,47

26,2

83,

111,557» 112.

Дата добавления: 2014-01-07