Лекция 6. Устойчивость грунтовых откосов

Массив грунта при определенных условиях может потерять устойчивость и в результате этого перейти из состояния статического равновесия в состояние движения. Такое состояние грунтового массива называется оползнем. Принятая классификация оползней основана на схемах потери устойчивости грунтового массива. Различают следующие виды оползней: оползни вращения; оползни скольжения; оползни разжижения (рис 6.1).

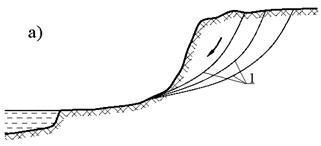
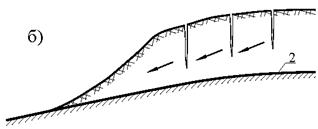
Рис. 6.1. Виды оползней: а – оползень вращения; б – оползень скольжения (пристенный оползень); 1 – поверхности скольжения в теле оползня; 2 – стационарная плоскость скольжения на границе оползня с подстилающим устойчивым массивом

Для оползней вращения характерна форма потери устойчивости грунтового массива в виде движения по криволинейной поверхности с вращением. Оползни скольжения называют также пристенными оползнями, так как их движение при нарушении равновесия происходит по заранее известным плоскостям, являющимся плоскостями контакта грунтового массива с устойчивыми горными породами. Оползнями разжижения называют грязевые потоки разжиженного водой грунта по выработанным руслам рек и тельвегам, например, селевые потоки. Механика грунтов изучает первые два типа оползней. Нарушение равновесия массива грунта может происходить внезапно со сползанием значительных масс грунта. Основными причинами нарушения равновесия массива грунта является увеличение нагрузок, действующих на массив, и уменьшение внутреннего сопротивления грунтового массива. Увеличение нагрузок может происходить по следующим причинам: возведение сооружений на откосах; водонасыщение массива грунта или подвешивание капиллярной влаги при понижении уровня грунтовых вод; увеличение градиента гидравлического напора и связанных с этой величиной фильтрационных сил. Фильтрационными силами называют силы давления и трения грунтового потока по поверхности минеральных частиц грунта. Интенсивности этих сил на единицу объема грунта могут быть вычислены по формулам:

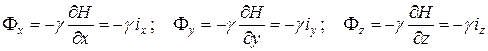, (6.1)

где H – гидравлический напор, выраженный в пьезометрических единицах, например, в метрах водяного столба.

Уменьшение сопротивления массива грунта может происходить в результате: разрушения естественных упоров, например, в результате подмыва основания откоса; уменьшения эффективного трения при возрастании порового давления; уменьшения сил сцепления при увлажнении и набухании грунтов. Ниже приводятся инженерные решения задач, связанных с определением устойчивости свободных откосов и склонов. Откос отличают от склона большим углом наклона свободной поверхности к горизонтали. По различным литературным источникам откосом называют склон с углом наклона свободной поверхности к горизонтали более 30°. Нормативная классификация грунтовых массивов, подразделяющая их на склоны и откосы отсутствует. В связи с эти приведенное выше определение откоса является условным.

1. Устойчивость откоса из идеально сыпучего грунта. Откос из идеально сыпучего грунта имеет свободную поверхность, наклоненную к горизонтальной плоскости под углом a (рис. 6.2).

Рис. 6.2. Предельное равновесие откоса, сложенного идеально сыпучим грунтом

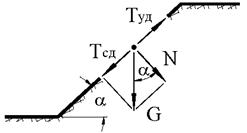
Элементарная частица грунта на свободной поверхности испытывает силу тяжести G, которую можно разложить на нормальную N и касательную T к наклонной поверхности компоненты:

(6.2)

Элементарная частица грунта удерживается на наклонной поверхности силой трения, равной произведению нормальной компоненты силы тяжести на коэффициент трения. Обозначим коэффициент трения как тангенс угла внутреннего трения j. Тогда из уравнения равновесия проекций всех сил на наклонную плоскость получим:

;

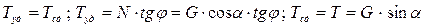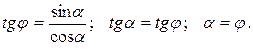(6.3)

Полученный результат можно обобщить в виде следующего определения: угол наклона к горизонтальной плоскости свободной поверхности откоса, сложенного идеально сыпучим грунтом, равен углу внутреннего трения этого грунта. Этот результат можно использовать в качестве теоретической основы экспериментального метода по определению угла внутреннего трения сыпучего грунта.

N_i

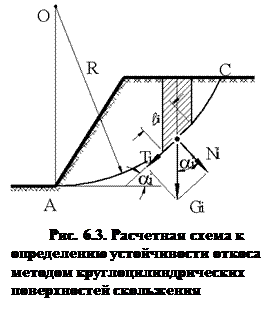2. Метод круглоцилиндрических поверхностей скольжения. Применяется для расчетов устойчивости оползней вращения. Основан на гипотезе, постулирующей круглоцилиндрическую поверхность скольжения, по которой происходит поступательно-вращательное движение верхней части грунтового массива при потере им устойчивости положения. Выберем на чертеже (рис. 6.3), изображающем вертикальный разрез откоса, бесконечно протяженного перпендикулярно плоскости чертежа, центр О кругло­цилиндрической поверхности скольжения. Будем предполагать (факт, установленный экспериментально), что плоскость скольжения проходит через основание откоса в точке А. Выделим верхнюю часть откоса окружностью радиусом ОА с центром в точке О, проходящей через основание откоса в точке А. Рассмотрим условие равновесия выделенной части откоса, для чего разделим ее вертикальными плоскостями, перпендикулярными чертежу, на элементарные объемы. Условие равновесия рассмотрим на примере i ^–го элементарного объема. Проведем центральную вертикальную ось площади этого объема и касательную к поверхности скольжения в точке ее пересечения с центральной осью. Обозначим угол наклона касательной к горизонтальной оси a_i. Вес элементарного объема грунта обозначим G_i и приложим в точке пересечения центральной оси с поверхностью скольжения. Разложим силу G_i на нормальную и касательную к поверхности скольжения составляющие N_i и T_i:

N_i = G_i cos a_i; T_i = G_i sin a _i. (6.4)

Сдвигающей силой является касательная составляющая силы тяжести T_сд,i = T_i. Удерживающими силами являются сила трения и сила сцепления по поверхности скольжения:

Т_уд,i = tg j_i G_i cos a_i + l_i c_i, (6.5)

где l_i – длина дуги поверхности скольжения в пределах i ^-го объема грунта;
c_i и j_i – сцепление и угол внутреннего трения грунта в пределах дуги l_i.

Условием равновесия по поверхности скольжения АС, пересекающей откос, является равенство нулю суммы моментов сдвигающих и удерживающих сил относительно центра О круглоцилиндрической поверхности скольжения:

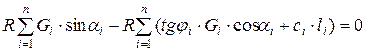. (6.6)

Для анализа устойчивости грунтового массива вместо уравнения (6.6) чаще всего используют выражение для коэффициента устойчивости, равное отношению момента удерживающих сил к моменту сдвигающих сил:

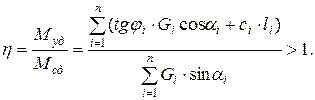(6.7)

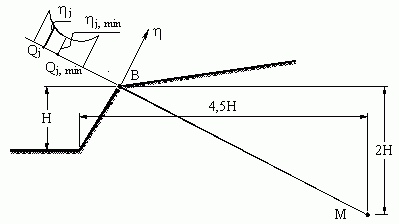
В формулах (6.6) и (6.7) угол a отсчитывается от горизонтали и считается положительным при повороте ее на острый угол до совмещения с касательной против хода часовой стрелки. При отрицательном угле a касательная составляющая силы тяжести и соответствующий ей момент являются удерживающими, что автоматически учитывается формулами (6.6) и (6.7). Предел суммирования по i n определяет количество элементарных объемов грунта, на которые разделяется верхняя часть откоса, отделенная от остального массива поверхностью скольжения. С увеличением n увеличивается точность расчетов по формулам (6.6) и (6.7). Формулы (6.6) и (6.7) являются не конечными, а промежуточными результатами. Решение задачи состоит в отыскании минимального коэффициента устойчивости откоса h для всех возможных траекторий поверхностей скольжения. Для упрощения решения поставленной задачи существуют следующие рекомендации. Предполагается, что центры возможных круглоцилиндрических поверхностей скольжения лежат на прямой (рис. 6.4), соединяющей вершину откоса В с точкой в глубине массива, отстоящей от основания откоса (точка А) по горизонтали на 4,5 Н и от верха откоса (точка В) по глубине на 2 Н. Варьируя на указанной линии положением центров поворота О_j, строят график зависимости коэффициента устойчивости откоса h_j от положения центра поворота О_j. Решением задачи (рис. 6.4) является минимальный коэффициент устойчивости откоса h_j,min.

А

Рис. 6.4. Расчетная схема к определению минимального коэффициента устойчивости

i

i

i

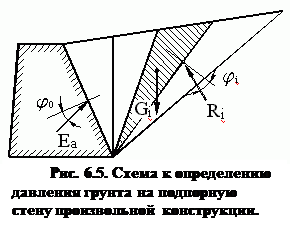3. Давление сыпучего грунта на подпорную стену произвольной конструкции. В этой задаче, в отличие от рассмотренной в лекции №5, под­порная стена и поверхность массива грунта могут иметь наклон, а на контакте стены с грунтом может реализоваться трение с условным углом внутреннего трения j₀. Задача решается построением веревочного многоугольника. Массив грунта за подпорной стеной разбивается лучами, исходящими из нижней точки подпорной стены, на элементарные тре­угольные призмы весом G_i (рис. 6.5). Век­тор реакции давления грунта на подпор­ную стену E_a отклонен от нормали к по­верхности подпорной стены на угол j₀ (рис. 6.6). Между элементарными тре­угольными призмами возникают давле­ния, вектор которых R_i отклонен от нормали к боковой грани призмы на угол внутреннего трения грунта j_i. Поверхность скольжения постулирована пло­ской, совпадающей с боковой гранью одной из призм, проходящей через осно­вание подпорной стены. Решение задачи формулируется следующим образом: по направлению и модулю вектора G_i и направлениям векторов Е_i и R_i опреде­лить модули векторов Е_i и R_i. Выполняя графические построения по сформули­рованному алгоритму, определяем вектора давлений на подпорную стену Е_i. Решением задачи (рис. 6.7) будет максимальное значение вектора Е_i,max, а соот­ветствующая ему плоскость скольжения будет расчетной плоскостью, по кото­рой наступает предельное равновесие грунтового массива.

a

Рис. 6.6. Схема к определению угла отклонения вектора активного давления грунта при наличии трения на контакте грунта с подпорной стеной

	Рис. 6.7. Графический метод определения давлений грунта на подпорную стену произвольной конструкции

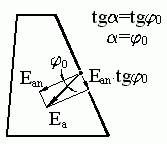
4. Расчет устойчивости пристенного оползня. Как уже отмечалось, предельное равновесие пристенного оползня реализуется по заранее известным плоскостям скольжения (рис. 6.8), каковыми являются плоскости контакта грунтового массива с коренными породами.

Y

Рис. 6.8. Схема определения оползневого давления

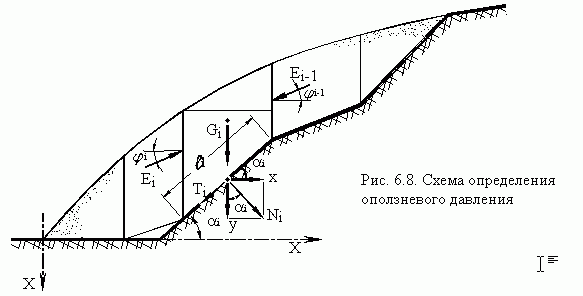
Решение задачи сводится к определению величины оползневого давления Е_i. Массив грунта разбивается вертикальными плоскостями, перпендикулярными чертежу, на элементарные призмы с приведенным весом G_i. Под приведенным весом понимается собственный вес грунта с нагрузкой на его поверхности. В пределах элементарной призмы поверхность скольжения должна быть представлена плоскостью (без переломов и изгибов). Предполагается, что силы оползневых давлений Е_i наклонены к боковым граням элементарных призм грунта под углом внутреннего трения j_i. Плоскость скольжения элементарной призмы наклонена к горизонтали под углом a_i. Решение задачи сводится к определению оползневого давления Е_i по известному давлению Е_i-1 и приведенному весу G_i. Для этого составляется и решается уравнение предельного равновесия на площадке скольжения. Приведем силы, действующие на элементарную призму (рис. 6.8), к их проекциям на вертикальную Y и горизонтальную X оси:

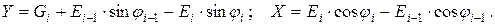(6.8)

Приведем систему сил (6.8) к их проекциям на нормаль к плоскости скольжения N и касательную T, лежащую в этой плоскости:

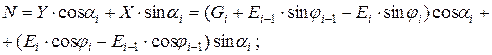
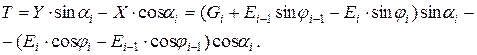(6.9)

Условие предельного равновесия на площадке скольжения будет иметь вид:

;

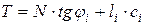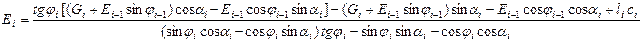
(6.10)

Полученное решение для Е_i используется для анализа устойчивости пристенного оползня следующим образом.

Для первой призмы в верхней части оползня принимается Е₀ = 0. Опреде­ляется по формуле (6.10) Е₁. Указанная процедура продолжается до тех пор, пока не будет вычислено Е_n – оползневое давление на свободной поверхности последней призмы нижней части оползня. Если Е_n больше нуля, оползень счи­тается неустойчивым. Если Е_n меньше нуля, устойчивость оползня обеспечена.

Дата добавления: 2014-01-07