Перераспределение инвестиций на основе трехсекторной модели

Выбор варианта желаемого развития региона

Структура регионального производства с точки зрения результата (валового продукта или национального дохода) может быть представлена элементами, которые выражают, с одной стороны, функциональную роль каждой его части в ходе воспроизводства, и, с другой - внешние формы этих частей продукта. При оптимальной структуре рационально используются все ресурсы и достигается наибольший прирост национального дохода.

Проблемы структуры исследуются в работах многих экономистов. Чаще всего принятие управленческих решений связано с изменением отраслевой структуры для повышения эффективности экономики региона.

Сформулируем несколько общих положений, которые помогут понять логику принятия решений по выбору варианта желаемого развития региона.

Во-первых, суммарные расходы бюджета региона, функционирующего на принципах самофинансирования, не должны превышать суммарных доходов; последние, если их рассматривать за продолжительный период, в котором нивелируются положительные и отрицательные флуктуации, не могут превышать величину национального дохода, создаваемого в отраслях материального производства.

Во-вторых, при принятии решений региональной значимости применяется сценарный подход. Например, меняя распределение ресурсов между отраслями или во времени, или задавая разные экономические нормативы ЛПР, естественно, будет получать различные результаты. Каждый результат социально-экономической политики формируется в процессе развития по конкретному варианту, вошедшему в определенный сценарий. Конкретному варианту можно присваивать трехзначный шифр: первая цифра обозначает номер сценария; вторая и третья - порядковый номер варианта внутри сценария. Например, вариант 151 расшифровывается как «пятьдесят первый вариант первого сценария». Варианты развития региона сравниваются между собой по совокупности критериев.

В-третьих, при изучении результатов расчетов по конкретному варианту исходят из того, что сложившиеся в прошлом тенденции в значительной мере будут сохраняться в переходном периоде.

В-четвертых, результаты каждого варианта исследуются на «сбалансированность» между: 1) масштабами производственной деятельности отраслей и их материальным обеспечением; 2) выпуском продукции и ее использованием на потребление и накопление; 3) потребностями в капвложениях на накопление производственных фондов.

Если рассчитанный вариант развития региона не удовлетворяет ряду требований (в частности, возможности самостоятельно развиваться в изменяющейся организационно-экономической среде; сбалансированности) в аналитическое исследование требуется включить другие варианты и выбрать из них такой, который удовлетворит критериям и ограничениям на ресурсы.

Примем, что отраслевая структура рационального варианта должна обеспечить достижение неких целей, которые стоят перед региональной экономикой. Во-первых, рост сальдо «вывоза-ввоза». Во-вторых, рост национального дохода на душу населения. Первая цель обусловливает высокие ранги сырьевых отраслей, так как в них формируется основная масса валового общественного продукта, предназначенного для вывоза за пределы региона. Но движение экономики по пути, задаваемому этой целью, сохраняет сырьевую специализацию хозяйственной деятельности региона. Вторая цель достигается экономией ресурсов всех видов. Удорожание стоимости живого труда, наблюдаемое во всех регионах России, высокие затраты на воспроизводство рабочей силы актуализируют, прежде всего, замещение живого труда овеществленным.

Новые капитальные вложения в основные производственные фонды повышают фондовооруженность, снижают затраты живого труда на единицу создаваемой продукции. Другими словами, трудовые ресурсы и основные производственные фонды взаимозаменяемы - показателем служит норма замены. Ее количественное значение - объем фондов, который надо направлять в отрасль на увеличение фондовооруженности труда для высвобождения единицы рабочей силы при условии, что производственный результат при этом не изменится.

Для выбора желаемого варианта желателен многокритериальный подход; в качестве критериев можно привлечь следующие показатели: «норма замещения» живого труда овеществленным; коэффициент абсолютных структурных сдвигов; коэффициент прогрессивности структуры; «векторный» критерий; прирост национального дохода; критерий Хаукинса-Саймона.

1. Показатель «норма замещения» определяется по формуле:

НЗ(t, t-1) = [Ф(t)-Ф(t-1)] / [(П(t)/П(t-1))-1].

где НЗ(t, t-1) – норма замены за период от t-1 до 1;

ФВ(t) и ФВ(t-1), ПТ (t) и ПТ (t-1)– фондовооруженность и производительность труда в конце и начале периода соответственно.

В условиях дефицитности производственных ресурсов показатель «норма замещения» используют при выработке структурной политики. Действительно, выяснив, в каких отраслях хозяйственного комплекса региона требуется наименьшее количество дополнительных фондовых средств для роста производительности труда, можно говорить о целесообразности направления туда дополнительных фондовых средств. В тех отраслях, где показатель «нормы» высок, предпочтительнее изыскать иные источники повышения производительности труда, нежели повышение его фондовооруженности.

2. Каждый регион как социально-экономическая система непрерывно меняет отраслевую структуру, регулирует собственное развитие. Уместно в связи с этим каким-либо способом измерять с определенной периодичностью интенсивность структурных преобразований (структурных сдвигов).

Показатели структурных сдвигов типа «абсолютный прирост» или «темп роста удельного веса» отражают изменения в удельных весах отдельных отраслей. Однако эти показатели не информативны для оценки структурных сдвигов, их «резкости» за конкретные периоды. Принято считать, что для решения этих задач удобно применять линейный или квадратичный коэффициенты «абсолютных структурных сдвигов» (АБС). Критерий АБС рассчитывается по формуле:

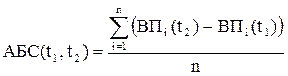
где i = 1, 2,.....,n – число отраслей регионального хозяйственного комплекса, включенное в модель; ВП_i(t₂) и ВП_i(t₁) - соответственно валовые объемы производства в отрасли в моменты t₂ и t₁.

Если показатель АБС увеличивается, это является свидетельством более интенсивных структурных сдвигов в данном варианте развития.

3. Коэффициент «прогрессивности структуры» позволяет устранить недостатки, присущие первым двум критериям. Главный из недостатков - оторванность критериев от целей, стоящих перед региональной экономикой. Попытаемся решить такую задачу прямо: включим в критерий оба показателя, принятые в качестве целевых, а именно – сальдо «вывоза-ввоза» (С) и национальный доход – НД. Для обеспечения сопоставимости оба показателя рекомендуется рассчитывать относительно одного жителя региона.

В общем случае возможны четыре парных сочетания этих показателей:

1. С(t₂) - С(t₁) > 0 НД(t₂) - НД(t₁) > 0;

2.С(t₂) - С(t₁) < О НД(t₂) - НД(t₁) ³0;

3. С(t₂) - С(t₁) ³О НД(t₂) - НД(t₁) < 0;

4. С(t₂) - С(t₁) <О НД(t₂) - НД(t₁) < 0.

Первое сочетание характеризует «абсолютно прогрессивную» перестройку отраслевой структуры, четвертое - «абсолютно регрессивную», второе и третье – «неопределенную». Варианты развития экономики региона, обеспечивающие «абсолютно прогрессивную» структуру, принимаются к рассмотрению; варианты с «абсолютно регрессивными» структурами отклоняются; до использования вариантов с «неопределенными» структурами проводятся дополнительные исследования с применением более сложных индексов (критериев).

Критерий прогрессивности структуры (ПС) за период t₁, t₂ рассчитывается по формуле:

,

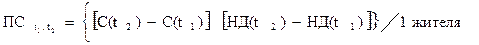В этой формуле синтезированы два целевых базисных показателя. Все, что возможно при их вычислениях, допустимо и при вычислении критерия «ПС». Элемент «С» отражает возможности экономики района обеспечивать население товарами и услугами, а отраслевые комплексы – сырьем, материалами и оборудованием; элемент «НД» отражает возможность экономики удовлетворить воспроизводственные потребности населения и отраслевые комплексы в финансовых ресурсах.

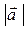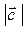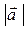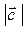4. «Векторный» критерий сконструирован геометрическим способом. Отраслевую структуру отобразим вектором, интенсивность структурных изменений – длиной вектора , направления структурных изменений – углом поворота вектора . Значения ирассчитываются по формулам:

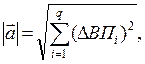
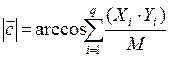
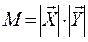, где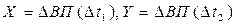

, ,

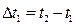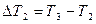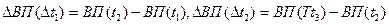
«Векторный» индекс является удобным инструментом для обоснования кратчайшего пути развивающейся региональной экономики к намеченной отраслевой структуре к концу прогнозного периода.

Охарактеризуем кратко возможности этих критериев.

Критерий «норма замещения» (НЗ) позволяет увидеть «общую панораму» региональной экономики, выявить группы отраслей, в которые было бы выгодно вкладывать капитал, применяя определенную экономическую политику. Критерий «абсолютный структурный сдвиг» (АБС) в экономических исследованиях применяется с давних пор; он не сложен в вычислениях и вместе с тем формален, т.е. несмотря на внешнюю формальную атрибутику весьма поверхностно характеризует структурные сдвиги, не раскрывает их сущность. В отличие от АБС – критерия третий («прогрессивность структуры» - ПС) экономически обоснован строже, так как базируется на системе моделей, описывающих региональное развитие. Четвертый критерий, «векторный», выполняет две функции. Прежде всего, он несет эмоциональную нагрузку, позволяет отслеживать траекторию прогнозируемого развития экономики. Вторая функция заключается в том, что движение по «кратчайшему пути» ликвидирует повороты траектории, неизбежные при поиске рациональной структуры с помощью трех первых критериев.

Все четыре критерия гармонично дополняют друг друга и помогают выбрать рациональный вариант, но все же не дают ответ на следующий актуальный вопрос: каковы доли различных факторов производства в конкретном варианте?

5. Пятый критерий выбора эффективного варианта регионального развития базируется на методе элиминирования отдельных факторов экономического роста, созданном группой исследователей под руководством Б.П. Плышевского. По каждому варианту развития в динамике рассчитываются приросты (абсолютные и относительные) национального дохода: общие; за счёт используемых трудовых ресурсов; за счёт используемых производственных фондов; за счёт эффективности производства.

6. Дополнительным критерием эффективности варианта может служить критерий Саймона-Хаукинса, тесно связанный со структурой межотраслевого баланса.

Народное хозяйство подразделено на n+1 сектор (n отраслей или производственных секторов и (n+1) -й – сектор конечного спроса). Для целей математических преобразований физический выпуск сектора i обычно обозначается через x_i; символ x_ij представляет количество продукции сектора i, используемой в качестве затрат сектором j. Количество продукции сектора i, доставляемое сектору конечного спроса x_{i n+1}, обычно обозначается для краткости как y_i.

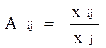
Объём выпуска сектора i, используемого сектором j при производстве единицы его совокупного выпуска j, обозначается символом a_ij и называется коэффициентом прямых затрат продукта i в секторе j: Коэффициенты прямых затрат – для аналитических целей – должны интерпретироваться как отношения двух количеств, измеренных в физических единицах. Только в том случае, если все элементы A_ij обратной матрицы неотрицательны, для любого заданного множества конечных поставок y₁,y₂,...,y_n, всегда существует комбинация положительных совокупных выпусков x₁,...,x_n, способных обеспечить эти поставки. Достаточным условием выполнения этого требования является положительность определителя матрицы:

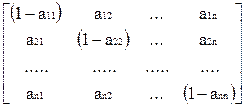
и всех её главных подматриц,

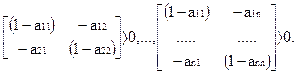
Если условие Хаукинса-Саймона выполняется хотя для одной произвольно пронумерованной последовательности секторов, то безусловно выполняется и для любой другой последовательности. Интерпретация этого условия такова: если экономическая система, в которой каждый сектор функционирует, непосредственно или косвенно потребляя продукцию других секторов, должна обеспечивать саму себя, и осуществлять положительные поставки для конечного спроса, то и любая из её подсистем должна быть способна осуществлять то же самое. Достаточное, но необходимое условие способности к самоподдержке экономики состоит в требовании, чтобы сумма коэффициентов каждого столбца структурной матрицы была не больше единицы и по крайней мере одна из столбцовых сумм была строго меньше единицы, т.е. .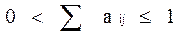

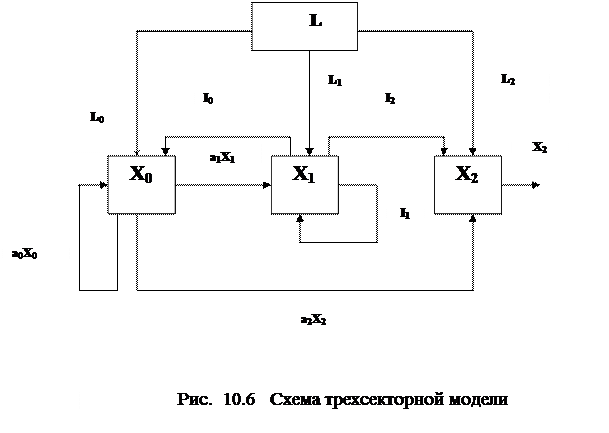
Рассмотрим трехсекторную модель регионального хозяйственного комплекса. Нулевой (материальный) сектор производит предметы труда; первый (фондосоздающий) – средства труда; второй (потребительский) – предметы потребления. Материальный сектор занимает промежуточную позицию между фондосоздающим и потребительским секторами: в определенном отношении его поведение сходно с поведением потребительского сектора, хотя по назначению он родственен фондосоздающему сектору. В этот сектор входят: добывающая промышленность, электроэнергетика, металлургия, промышленная химия и нефтехимия, производство сельхозпродукции, лесозаготовки, промышленность стройматериалов, грузовой транспорт, оптовая торговля средствами производства.

В фондосоздающий сектор входят: металлообработка и машиностроение (выделим такую подотрасль как машиностроение для сельского хозяйства), промышленное строительство; потребительский сектор: переработка сельхозпродукции (легкая и пищевая промышленность), деревообработка, бытовая химия, гражданское строительство, пассажирский транспорт, торговля предметами потребления.

Предположим, что за каждым сектором закреплены основные производственные фонды, в то время как труд и инвестиции могут свободно перемещаться между секторами. Производственные возможности каждого сектора заданы в форме линейно-однородных производственных функций:

X_j=F_j(K_j,L_j), j=0,1,2,

где X_j , K_j,L_j , -соответственно выпуск, основные производственные фонды и число занятых в j-том секторе.

Модель включает следующие уравнения:

L=L(0)e^vt (число занятых)

L₀+L₁+L₂=L (распределение занятых по секторам)

dK_j/dt= -m_j*K_j+I_j, K_j(0)=K_j0, j=0,1,2 (динамика фондов по секторам);

X_j=F_j(K_j,L_j), j=0,1,2 (выпуск продукции по секторам);

X₁=I₀+I₁+I₂ (распределение продукции фондосоздающего сектора);

X₀=a₀X₀+a₁X₁+a₂X₂ (распределение продукции материального сектора),

где I_j –инвестиции в j-тый сектор; v –темп прироста занятых; m_j- коэффициенты выбытия основных производственных фондов по секторам; a_j –коэффициенты прямых материальных затрат по секторам.

На рис. 10.6. приведена схема трехсекторной модели в натурально-вещественной форме. В относительных показателях модель принимает следующую форму:

q₀+q₁+q₂=1, q_j>0, j=0,1,2,

s₀+s₁+s₂=1, s_j>0, j=0,1,2, (1)

dk_j/dt=(q₁*s_j/q_j)*f₁(k₁)-l_j*k_j, k_j(0)=k_j0, l_j= v + m_j, j=0,1,2,

(1-a₀)*q₀*f₀(k₀)=a₁*q₁*f₁(k₁)+ a₂*q₂*f₂(k₂),

где q_j=L_j/L –доля числа занятых в j-том секторе в общем числе занятых;

s_j-доля инвестиций в j-тый сектор в общем объеме инвестиций;

f_j(k_j)=X_j/L_j – производительность труда в j-том секторе.

Последнее уравнение системы (1) можно записать в следующей форме:

(1-a₀)x₀ = a₁x₁+a₂x₂, где (2)

x_J=X_j/L - народнохозяйственная производительность j-того сектора, т.е. выпуск продукции j-того вида на одного занятого, при этом

x_j = q_jf_j(k_j).

В системе (1) параметры a_0,a₁, a₂, m₀,m₁,m₂, v являются экзогенными и считаются постоянными. Параметры (q,s)- управляющие. Уравнения фондовооруженности принимают следующий вид:

S1*f1(k₁⁰)= l₁*k₁⁰, k_j⁰= (q₁*s_j)/(q_j*l_j)*f(k₁⁰), j=0,2.

При k_j< k_j⁰, как видно из (1), dk_j/dt>0, а при k_j> k_j⁰ значения dk_j/dt <0, поэтому

lim k_j(t)= k_j⁰ (3)

Докажем, что путем регулируемого перераспределения труда и инвестиций можно обеспечить монотонный рост экономики по всем секторам. Допустим, что производственные функции секторов – это функции Кобба-Дугласа

F_j(K_j,L_j) =A_jK_j^aL_j^1-a, f_j(k_j)= A_j k_j^a,

(для сокращения записи вместо A_j k_j^a иногда будем употреблять f_j(k_j)).

Базовые начальные условия- L(0),K₀(0), K₁(0), K₂(0), а начальная фондовооруженность k_j(0) –уже производная от базовых и зависит от того, как выбраны управляющие параметры в начальный момент t=0. Выберем их так, чтобы выполнялся материальный баланс и k_j(0) < k_j⁰, j=0,1,2.

Согласно (1),условия k_j (0) < k_j⁰ и dk_j (0) / dt>0 эквивалентны, поэтому надо так выбрать (q,s), чтобы dk_j (0) / dt>0, т.е.

(q₁*s_j)/q_j*f₁[k₁(0)]- l_j*k_j(0) >0, j=0,1,2, или

s_j>(q_j l_jk_j(0))/ q₁f₁[k₁(0)]= l_jK_j(0)/ A₁K_j^a1(0)[ q₁L(0)]^1-a, j=0,1,2. (4)

Это означает, что в начальный момент выпуск средств труда превышает объем поддерживающих капитальных вложений; при выполнении этих условий в сбалансированной по труду и инвестициям экономике наблюдается рост.

Варьируя переменными «труд» и «инвестиции», можно привести трехсекторную экономическую систему в сбалансированное стационарное состояние. С экономической точки зрения стационарное состояние- это состояние расширенного воспроизводства, когда инвестиции расходуются на замену выбывших средств труда и частично на такое расширение производственных фондов, которое обеспечивает сохранение фондовооруженностей на постоянном уровне, несмотря на рост занятых с постоянным темпом.

Если производственные функции секторов задаются в виде уравнений Кобба-Дугласа, то в сбалансированном состоянии при заданном распределении труда и инвестиций между секторами экономика характеризуется показателями, приведенными в табл.10.1

Таблица10.1

Показатели, характеризующие стационарное (сбалансированное) состояние экономики

Наименование сектора	Фондовооруженность	Производительность труда
Материальный	s0q1 k0= * A1k1^a^1 l0q0	x0=q0 A0k0^a^0
Фондосоздающий	s1A1 ^1 / (1-^a^1) k1= l1	x1=q1 A1k1^a^1
Потребительский	S2q1 k2= * A1k1^a^1 l2q2	x2=q2 A2k2^a^2

Если в выражения для удельных выпусков в табл.10.1 подставить значения стационарной фондовооруженности из этой же таблицы, то удельные выпуски примут вид функций от параметров распределений труда (q₀,q₁,q₂) и инвестиций (капитальных вложений) (s_0,s_1,s₂):

x₀=B₀ q₀^1-a0 q₁^a0 s₀^a0s₁^{(a1 a0) / (1 - a1)},

x₁= B₁ q₁ s₁^{a1 / (1 - a1)}, (5)

x₂= B₂ q₂^1-a2 q₁^a2 s₂^a2s₁^{(a1 a2) / (1 - a1)},

где В₀=A₀A^{a0/ (1 - a1)} l₀^{- a0} l₁^{(a1 a0) / (1 - a1)}

B₁= A₁^{1/ (1 - a1)} l₁ ^{a1 / (1 - a1)}

B₂= A₂A₁^{a2/ (1 - a1)} l₂^{- a2} l₁^{(a1 a2) / (1 - a1)}

Условия сбалансированности по труду, инвестициям и материалам, как и выше, записываются следующим образом:

q₀+q₁+q₂=1, q_j>0 (труд)

s₀+s₁+s₂=1, s_j>0 (инвестиции) (6)

(1-a₀)x₀ = a₁x₁+a₂x₂ (материалы)

Материальный баланс как уравнение связи между q_0, q_1, q_2, s_0, s_1, s₂ принимает вид (7):

(1-a₀)B₀ q₀^1-a0 q₁^a0 s₀^a0s₁^{(a1 a0) / (1-a1)} =

=a₁B₁q₁s₁^a1/(1-a1)+a₂B₂q₂^1-a2 q₁^a2s₂^a2s₁^{(a1 a2)/(1-a1)} (7)

Таким образом, любое сбалансированное стационарное состояние трехсекторной экономики – это некоторая точка (q_0, q_1, q_2, s_0, s_1, s₂) в шестимерном пространстве, координаты которой удовлетворяют трем натуральным балансам.

Основным управляющим воздействием со стороны региональных органов власти должно быть регулирование трудовых и инвестиционных ресурсов. Так как главной целью субъекта управления является улучшение благосостояния населения региона, то при примерном постоянстве доли занятых в общей численности населения это означает необходимость максимизировать производство предметов потребления на одного занятого в материальном производстве.

Приняв во внимание это соображение, целевую задачу можно сформулировать следующим образом:

max q₁^a2 q₂^1-a2 s₁^{(a1 a2)/(1-a1)} s₂^a2 (8)

при условии, что компоненты (q,s)= (q_0, q_1, q_2, s_0, s_1, s₂) связаны соотношениями (6). Решение этой задачи и определит “золотое” правило распределения трудовых и инвестиционных ресурсов между секторами.

Задача (8) решается в два этапа:

1) находится максимум удельного потребления при фиксированных q₀ и s₀, игнорируя при этом выполнение материального баланса;

2) варьируя q₀ и s₀, необходимо добиться выполнения баланса и вычислить искомый максимум.

Максимум функции (10) при условии q₁+q₂=1-q_0, s₁+s₂=1 - s₀ достигается для следующих значений управляющих параметров:

q₁^*=a₂(1-q₀), q₂^*=(1-a₂)(1--q₀),

s₁^*=a₁(1-s₀), s₂^*=(1-a₁) (1-s₀) (9)

На втором этапе надо найти

max (1-q₀) (1-s₀) ^a2/(1-a1) , 0<q₀ , s₀<1 (10)

Решая уравнение материального баланса относительно q_0, получим q₀(0)=1, q₀(1)=0, q^/₀(s₀) <0 поэтому удельное потребление x₂(s₀) достигает своего максимального значения в единственной точке s₀^*, определяемой из уравнения

[a₂/(1-a₂)][1-q₀ (s₀)]=- q^/₀(s₀)(1- s₀) (11)

Таким образом, находим точку искомого максимума

q₀^*=q₀(s₀^*), q₁^* = a₂(1-q^*₀), q₂^*=(1-a₂)(1--q^*₀),

s₀^*, s₁^*=a₁(1-s₀^*), s₂^*=(1-a₁) (1-s₀^*)

Дата добавления: 2014-01-07