Лекция 1. Характеристики электрических полей

Усачев Е.Е.

Методы расчета электрических полей

Конспект лекций

по курсу

Казань 2008

УДК 621.373(075.8)

ББК 31.247-5

У-74

Конспект лекций по курсу «Методырасчета электрических полей». Казань: Казан. гос. энерг. ун-т, 2008. - с.

Курс «методы расчета электрических полей» относится к циклу естественно научных дисциплин и предусматривает более детальное знакомство студентов с методами расчетов электрических полей, чем это проводилось в рамках изучения физики в разделе «Электричество». Курс является одним из базовых при подготовке дипломированных специалистов по специальности 140201 «Высоковольтная электроэнергетика и электротехника» в Казанском государственном энергетическом университете. В рамках данного курса студенты знакомятся с такими аналитическими методами расчета полей как: метод суперпозиции, метод отражения, метод конформных преобразований и др. Рассмотрены численные методы расчета: дифференциальный метод, метод конечных элементов, метод эквивалентных зарядов. Уделяется внимание оценке характеристики поля по его графической картине и нахождению максимально допустимого напряжения сложных электродных систем по коэффициенту неоднородности поля.

_________________

Рецензенты:

Д-р тех. наук, проф. И.М.Валеев

Рекомендовано секцией РИС электроэнергетического института.

Председатель секции В.Л. Матухин

ã Казанский государственный энергетический университет, 2008

Поле (физическое) – это первичная физическая реальность, одна из форм существования материи, способ передачи взаимодействия между различными телами.

Поле (математическое) – пространство, в котором каждой точке сопоставлено значение некоторой физической величины (скалярной, векторной). Соответствующие поля называются скалярными или векторными. Примеры скалярных полей: поле температур (в прогнозе погоды), поле распределения масс (плотность). Примеры векторных полей: поле скоростей движения частиц в потоке жидкости или газа.

Электростатическое поле является частным случаем электромагнитного поля. Оно создается неподвижными электрическими зарядами и у него отсутствует магнитная составляющая. Электростатическое поле является полем векторным. Каждой точке пространства сопоставлен вектор электрического поля, который называется напряженностью электрического поля. Этот вектор обозначается символом Е и имеет размерность вольт/метр.

Если в каждой точке векторного поля определена скалярная переменная, то такое векторное поле называется потенциальным. Высота точки на местности определяет скалярный потенциал поля сил земного тяготения (гравитационного поля). Электрическое поле характеризуется наличием скалярного электрического потенциала в каждой точке пространства. Потенциал является энергетической характеристикой электрического поля и определяется работой, которую необходимо совершить против сил поля для того, чтобы переместить положительный единичный заряд из точки, где потенциал принят равным 0, в данную точку. Поля такого рода (потенциальные) называют также безвихревыми полями.

В безвихревом поле можно найти множество точек, скалярные потенциалы которых одинаковы. Такие точки расположены на какой-то, в общем случае криволинейной, поверхности, называемой эквипотенциальной поверхностью (поверхностью уровня). Любая линия, проведенная на эквипотенциальной поверхности, называется эквипотенциальной линией (линией уровня). При графическом изображении электростатического поля с помощью эквипотенциальных линий придерживаются следующего правила: разность потенциалов между двумя соседними эквипотенциальными линиями выбирается постоянной. Такое изображение поля дает наглядное представление о характере распределения потенциала и скорости его изменения: дальше эквипотенциальные линии расположены друг от друга – меньше скорость изменения потенциала (gradf, напряженность) и наоборот.

Вектор, показывающий наибольшую скорость пространственного изменения потенциала f в данной точке, называется градиентом потенциала и обозначается либо символом gradf, либо (более кратко) Ñf (набла). Слово градиент происходит от латинского слова gradientis (шагающий) и введено Максвеллом в 1873 г. Градиент потенциала это силовая характеристика электростатического поля, которая является векторной величиной. Как и любой вектор, его можно разложить на составляющие по координатным направлениям, каждая из которых равна скорости изменения величины потенциала в соответствующем направлении. Вид градиента в различных системах координат приведен в (1.5).

В ДСК gradf ºÑf = ¶f/¶ x × i + ¶f/¶ y × j + ¶f/¶ z × k

В ЦСК gradf ºÑf = ¶f/¶ r 1 _r + 1/ r ׶f/¶q× 1_q + ¶f/¶ z × k (1.5)

В ССК gradf ºÑf = ¶f/¶ r 1 _r + 1/ r ׶f/¶q× 1_q + 1/(r ×Sinq)׶f/¶j× 1_j

Из уравнений (1.5) следует, что вычисление градиента является операцией дифференцирования скалярной величины потенциала по координатам. Для обозначения этой операции можно применить краткий символ Ñ, приписываемый перед символом той величины, от которой берут градиент. Символ Ñ называют дифференциальным оператором (“набла”). Вектор градиента Ñf (gradf) можно рассматривать как произведение формального “вектора” Ñ на скалярную величину потенциала f.

Ñ = ¶/¶ x × i + ¶/¶ y × j + ¶/¶ z × k

Ñ = ¶/¶ r 1 _r + 1/ r ׶/¶q× 1_q + ¶/¶ z × k (1.6)

Ñ = ¶/¶ r 1 _r + 1/r׶f/¶q× 1_q + 1/(r ×Sinq)׶/¶j× 1_j

Величина градиента потенциала тем больше, чем ближе расположены друг к другу эквипотенциальные поверхности (или линии), соответствующие значениям потенциала, отличающимся на одну и ту же величину. Направление градиента потенциала всегда нормально (перпендикулярно) к эквипотенциальной поверхности (или линии), проходящей через данную точку. Градиент потенциала электростатического поля равен пределу отношения силы, с которой поле действует на отрицательный пробный заряд, к величине этого заряда при неограниченном уменьшении величины последнего (чтобы искажением поля, вносимым присутствием пробного заряда, можно было пренебречь). Если бы пробный заряд не обладал инерцией, то его движение под действием сил поля происходило бы по некоторой линии, называемой линией поля или силовой (векторной) линией. Градиент потенциала в любой точке направлен по касательной к линии поля. Величина градиента потенциала электрического поля, взятая с обратным знаком, называется напряженностью электрического поля (Е). Она равна пределу отношения силы, с которой поле действует на положительный пробный заряд, к величине этого заряда при неограниченном уменьшении величины последнего. Знак минус между напряженностью и градиентом потенциала возникает из того, что в качестве пробных зарядов берутся заряды разных знаков.

E = -gradf º -Ñf = -(¶f/¶ x × i + ¶f/¶ y × j + ¶f/¶ z × k) = E_x × i + E_y × j + E_z × k (1.7)

E_x = -¶f/¶ x; E_y = -¶f/¶ y; E_z = -¶f/¶ z

Кроме потенциала и напряженности (градиента потенциала) для характеристики любого векторного поля вводится ряд других понятий:

1. Векторная линия (силовая линия, линия поля, линия тока).

2. Векторная трубка.

3. Поток векторного поля.

4. Циркуляция векторного поля.

5. Дивергенция векторного поля.

6. Вихрь векторного поля.

Векторная линия – линия, касательная к которой в каждой точке поля совпадает с направлением вектора поля. Из такого определения векторной линии следует, что в любой её точке векторное произведение касательной к векторной линии и вектора поля равно нулю, т.е. дифференциальное уравнение векторной линии имеет вид:

, (1.8)

где а_х, а_y, а_z – координаты вектора поля; x, y, z – координаты точки векторной линии. Если векторное поле – поле скоростей частиц стационарного потока жидкости, то векторная линия – траектория частиц жидкости. При графическом изображении электростатического поля с помощью векторных линий (силовых линий) придерживаются следующего правила: число силовых линий поля, приходящихся на единицу площади, должно быть пропорционально напряженности электрического поля. Такое изображение поля дает наглядное представление о характере распределения напряженности: там, где линии расположены гуще – напряженность выше, а там, где линии расположены более редко – напряженность меньше.

Векторная трубка – это совокупность всех векторных линий векторного поля, проходящих через некоторую замкнутую кривую. Можно дать и другое определение векторной трубки как части пространства, состоящей из векторных линий. На рис.1.2а показана некоторая векторная трубка. Хотя площади сечений S ₁ и S ₂ не равны между собой, число силовых линий, проходящее через эти поверхности одинаково. Если пронумеровать все силовые линии, проходящие через поверхность S ₁, то окажется, что через любое сечение силовой трубки проходят все эти линии и никаких других. Число силовых линий в трубке постоянно.

Поток векторного поля. Элементарным потоком вектора называется скалярное произведение вектора на элемент поверхности. Произведение Е×ds = Е × ds × cos(Е,ds) – называется элементарным потоком электростатического поля. Потоком вектора через поверхность S называется сумма (интеграл) элементарных потоков через элементы поверхности dS. Если поверхность является замкнутой и ограничивает какой-либо выделенный элемент объема, то это обозначается кружком на знаке интеграла:

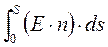, , (1.9)

где n – единичный вектор нормали к элементу поверхности dS. Для поля скоростей частиц жидкости поток равен количеству жидкости, протекающей за единицу времени через поверхность S. Поток по определению является скалярной величиной. Вычисление потока может производиться также через какую угодно замкнутую поверхность. Если густоту линий поля выбрать так, чтобы она соответствовала числовому значению вектора поля; то поток вектора можно условно представить количеством линий поля, пронизывающих рассматриваемую поверхность.

Циркуляцией (от латинского circulatio – вращение) векторного поля Е (r) вдоль некоторой кривой L называется интеграл вида

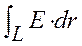(1.10)

Циркуляция поля вдоль кривой L равна работе, совершаемой силами векторного поля Е (r) при перемещении пробного тела (единичной массы, единичного заряда и т.д.) вдоль этой кривой L. По определению циркуляция является скалярной характеристикой поля.

Полный поток вектора через замкнутую поверхность, ограничивающую малый объем, может быть равен нулю или же отличаться от нуля. В первом случае говорят, что в объеме не содержится источника (стока), в котором линия поля могла бы начинаться (заканчиваться). Во втором – содержаться. Суммарное количество источников и стоков, находящихся внутри замкнутой поверхности определяет количество линий поля, выходящих (входящих) из объема, ограниченного этой поверхностью. Силовые линии электростатического поля начинаются на положительных зарядах, которые можно считать истоками, и заканчиваются на отрицательных, которые можно считать стоками электрического поля. Определив полный поток вектора через замкнутую поверхность, можно определить суммарное количество истоков и стоков поля, т.е. заряд, содержащийся в объеме, ограниченном данной поверхностью. Для характеристики поля принято определять количество истоков (стоков) линий поля в каждой точке (в предельно малом объеме) пространства поля. Эта характеристика называется дивергенцией. Дивергенция (расходимость) вектора равна пределу, к которому стремится отношение полного потока вектора через замкнутую поверхность к величине объема, ограниченного этой поверхностью, при бесконечном уменьшении последнего.

(1.11)

Дивергенция является скалярной величиной; она положительна, если линия поля начинается в малом объеме, или отрицательна, если линия поля в этом объеме заканчивается. -

Наличие дивергенции вектора всегда связано с наличием в данной точке источника или стока линий поля. В электрическом поле источниками являются положительные заряды, стоками - отрицательные. Следовательно, дивергенция вектора напряженности электростатического поля Ñ × E имеет отличное от нуля значение в пунктах расположения зарядов. В других местах электростатического поля, не содержащих зарядов, дивергенция отсутствует. В этом состоит ясный физический смысл дивергенции поля: дивергенция поля пропорциональна плотности зарядов. В магнитном поле дивергенция вектора магнитной индукции всегда равна нулю, т.к. магнитных зарядов в изолированном виде в природе нет.

Выделим в векторном поле произвольный замкнутый контур. Определим составляющую этого поля вдоль контура и проинтегрируем. Этот интеграл называется, как указывалось выше, циркуляцией поля по замкнутому контуру. В силовых полях он равен работе сил поля по произвольному замкнутому контуру. Работа сил поля по замкнутому контуру может либо равняться нулю, либо не равняться нулю. Например, без учета сил трения работа по произвольному замкнутому контуру в гравитационном поле равна нулю. В другом примере, при движении воды в водовороте работа по контуру водоворота не равна нулю. Попробуйте представить, что вы плывете в водовороте против течения, и вам станет ясно, что работа эта не будет равна нулю. Для характеристики векторного поля по отношению к работе, совершаемой по замкнутому контуру, вводится понятие вихрь или ротор. Ротор определяется как предел отношения работы сил поля (циркуляция вектора поля) по замкнутому контуру к площади, ограниченной этим контуром, когда последняя стремится к нулю.

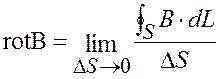(1.18)

Наглядно представить ротор можно следующим образом. Пусть мы имеем поле скоростей течения воды. Заморозим мысленно всю воду за исключением некоторой замкнутой трубки. Можно сказать, что ротор пропорционален скорости движения воды в этой трубке. Если вода не движется, то ротор равен нулю. Если вода движется, то ротор не равен нулю, а в этом месте образуется вихрь. Поля, в которых ротор не равен нулю, называются селеноидальными или вихревыми полями. Если дивергенция поля div Е может быть представлена как скалярное произведение оператора «набла» Ñ на вектор напряженности поля Е, то ротор представляет собой векторную характеристику и равен векторному произведению оператора «набла» Ñ на вектор напряженности поля Е

(1.19)

В выражении (1.19) приведен вид ротора в декартовой системе координат.

Вектор электрического смещения (электрической индукции)

Пусть на некоторую поверхность S помещен заряд Q. Выделим элемент этой поверхности dS с зарядом на нем dQ. Величиной смещения D называется предел отношения заряда dQ, находящегося на элементе поверхности dS, к площади поверхности dS, когда площадь стремится к нулю:

D = (1.22)

С другой стороны, этот предел отношения заряда к площади поверхности, на которую он помещен, называется поверхностной плотностью заряда. Смещение является векторной величиной, поскольку в определении смещения D заряд Q является скалярной величиной, а элемент поверхности dS – вектор. Вектор смещения перпендикулярен (направлен вдоль нормали) элементу поверхности. Связь между вектором электрического смещения D и вектором напряженности электрического поля задается выражением:

D =e₀e E, (1.23)

(ф/м), (1.24)

где e₀ - электрическая постоянная (абсолютная диэлектрическая проницаемость вакуума), измеряемая в фарадах/метр (ф/м) и равная отношению суммарного электрического заряда, заключенного в некотором объеме в вакууме, к потоку вектора напряженности электрического поля через замкнутую поверхность, ограничивающую этот объем; e - относительная диэлектрическая проницаемость среды, показывающая во сколько раз напряженность поля в среде меньше напряженности поля в вакууме.

Характерные признаки потенциального поля:

a. rotA º 0 – ротор равен нулю во всех точках поля;

b. divА ¹ 0 – дивергенция не равна нулю, хотя бы в некоторых точках поля;

c. A = grad b – в любой точке поля определен скалярный потенциал.

Условия существования вихревого поля:

a. divB º 0 – дивергенция равна нулю в любой точке поля;

b. B º rotA – ротор не равен нулю хотя бы в некоторых точках поля;

c. отсутствует скалярный потенциал.

Дата добавления: 2014-01-07