Тема 1.4 Средние величины и показатели вариации

Средние величины – наиболее распространенные обобщающие величины в статистике.

Средняя величина – это обобщающая характеристика совокупности однотипных явлений по какому-либо количественно-варьирующему признаку в расчете на единицу совокупности, в конкретных условиях места и времени.

На практике часто приходится рассматривать качественно неоднородные совокупности и рассчитывать их обобщающую среднюю величину.

Для того, чтобы средняя характеристика была достоверной величиной необходимо, чтобы ее построение было основано на массовом обобщении факторов.

1. Основная масса средних величин, которые рассматриваются в статистике относятся к классу так называемых степенных средних.

Общая их формула имеет вид:

,

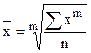где n – число единиц совокупности,

m – показатель степени.

В зависимости от этого показателя рассматриваются различные виды средних:

1. m=1, - средняя арифметическая.

2. m=2, 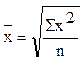- средняя квадратическая.

3. m=3, 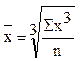- средняя кубическая.

4. m=-1, 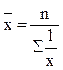- средняя гармоническая.

5. m=0, - средняя геометрическая.

Средняя арифметическая величина используется в двух формах:

а) В форме простой (1)

б) В форме средней арифметической взвешенной: (2)

Первая применяется тогда, когда все частоты равны 1 или равны между собой.

Во всех остальных случаях применяется формула (2).

ПРИМЕР: Вычислите средний стаж работы рабочего на основании следующих данных:

Стаж, лет х	Число рабочих, чел f	х*f

Решение:

Для расчета среднего стажа воспользуемся формулой средней арифметической взвешенной, т.к. частоты не равны единице и не равны между собой.

Вычисление средней в интервальном ряду:

Группы рабочих по размеру месячной оплаты труда, тыс.руб.	Число рабочих, чел. f	х	х*f
До 120 120-130 130-140 140-150 150-160 160-170 170-180 свыше 180
Итого:

Необходимо рассчитать среднюю заработную плату.

Чтобы вычислить среднюю в интервальном вариационном ряду нужно перейти от интервального к дискретному, взяв в качестве вариант середины интервала. Так как первый интервал открытый, то считаем, что он такой же по величине как последующий, а последний такой же, как предыдущий.

1-ый интервал: (110+1020)/2=115 и т.д.

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака.

Применяется в 2-х формах:

1) в форме простой;

2) в форме взвешенной.

1) ; 2)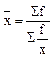

При выборе вида средней необходимо руководствоваться следующими правилами:

ПРАВИЛО 1: Если неизвестная величина стоит в числителе исходного отношения, то для расчета нужно применять среднюю арифметическую взвешенную, приняв в качестве весов слагаемые показатели стоящего в знаменателе.

ПРИМЕР: Имеются следующие данные по предприятиям отрасли:

Предприятие	План, т (f)	Степень выполнения плана, %
Итого		-

Найти средний процент выполнения плана.

Средний процент выполнения плана определяется следующим образом:

Фактическое выполнение плана:

ПРАВИЛО 2: Если неизвестная величина стоит в знаменателе исходного отношения, то для расчета следует применять формулу средней гармонической взвешенной, приняв в качестве весов слагаемые показателя, стоящего в числителе исходного отношения.

ПРИМЕР: Имеются следующие данные по предприятиям отрасли:

Предприятие	Фактический выпуск продукции, млн.руб., m	Степень выполнения плана, %
Итого		-

Найти средний процент выполнения плана.

Средний процент выполнения плана составляет:

Структурные средние: мода и медиана. Их вычисление в дискретных и интервальных вариационных рядах

Мода и медиана – особого рода средние, которые используются для изучения структуры вариационного ряда. Их иногда называют структурными средними, в отличии от рассмотренных ранее степенных средних.

Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. имеет наибольшую частоту.

Мода имеет большое практическое применение и в ряде случаев только мода может дать характеристику общественных явлений.

Медиана – это варианта, которая находится в середине (ранжированного) упорядоченного вариационного ряда.

Медиана показывает количественную границу значения варьирующего признака, которой достигла половина единиц совокупности.

Расчет моды и медианы в ранжированном и дискретном вариационных рядах:

ПРИМЕР: Имеются следующие данные по штамповочному цеху предприятия. Определите средний стаж работы по цеху:

Стаж, лет х	Число рабочих, чел f	Накопленные частоты
		2+4=6 2+4+5=(11) 2+4+5+4=15 2+4+5+4+1=16
-		-

Решение:

Представим исходный дискретный ряд в виде ранжированного ряда:

1, 1, 3, 3, 3, 3, 4, 4, 4, 4, 4, 8, 8, 8, 8, 10.

Рассмотрим все возможные подходы к определению моды и медианы:

1) Определим моду:

- в ранжированном ряде мода не определяется.

- в дискретном ряде мода М₀=4 (по определению).

2) Рассчитаем медиану:

В ранжированном ряду медианой будет средняя из двух вариант, находящихся в середине ряда, т.е. полусумме восьмого и девятого значений признака (Ме=4).

1, 1, 3, 3, 3, 3, 4, [4], [4], 4, 4, 8, 8, 8, 8, 10

1, 2, 3, 4, 5, 6, 7, (8), (9), 10,···

Для того, чтобы вычислить медиану в дискретном ряду, найдем предварительно половину суммы частот f/2=16/2=8. Если сумма частот является числом нечетным, то вначале прибавляем к этой сумме единицу, а затем делим пополам: (f+1)/2. Для того, чтобы определить, какая варианта будет являться медианой в дискретном ряду, будем накапливать частоты до тех пор, пока не полученная полусумма частот не будет равна или превышать полусумму частот. Соответствующая варианта и будет медианой.

Ме=4.

Половина рабочих имеет стаж меньше 4-х лет, половина больше, а 4 – находится в середине ранжированного ряда.

Вычисление моды и медианы в интервальном вариационном ряду:

Мода в интервальном вариационном ряду вычисляется по формуле:

,

Х_М - начальная граница модального интервала.

Нм – величина модального интервала.

fм₀, fм_0-1, fм₀₊₁ - соответственно частота модального интервала предшествующего модальному и последующего.

Модальным называется такой интервал, которому соответствует наибольшая частота.

Для интервального ряда Ме вычисляется по следующей формуле:

где Хм_е - нижняя граница медиального интервала,

hм_е – величина медиального интервала,

- половина суммы частот,

fм_е – частота медианного интервала,

Sм_е-1 – сумма накопленных частот интервала предшествующего медианному.

Медианный интервал – такой интервал, которому соответствует кумулятивная частота равная или превышающая половину суммы частот.

ПРИМЕР: Имеются следующие данные о распределении предприятий отрасли по среднегодовой стоимости основных фондов:

Группы предприятий по среднегодовой стоимости ОФ, ден.ед., x	Число предприятий, f
[39640-51685)
[51685-63730)
[63730-75775)
[75775-87820]
Итого

*Рассчитаем моду (Мо) и медиану (Ме):

Сначала определим модальный интервал, он соответствует наибольшей частоте. Наибольшая частота 7 является модальной, интервал [63730-75775) — модальный интервал. Затем подставим данные в формулу:

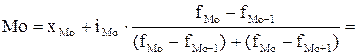
Определим медианный интервал. Полусумма частот равна 10 (Sf/2 = 20/2 = 10). Накапливая частоты, определим интересующий интервал (сумма накопленных частот 4 + 6 = 10), значит 6 является медианной частотой, а интервал [51685-63730) является медианным интервалом).

Затем подставим данные в формулу:

Вывод: Произведенные расчеты показывают, что наибольшее число предприятий имеет среднегодовую стоимость основных фондов около 66139 ден.ед.; у половины предприятий стоимость ОФ в среднем за год составляет менее 63730 ден.ед., а половина- более 63730 ден.ед.

Дата добавления: 2014-01-07