Показатели вариации. Задача статистики заключается в том, чтобы дать числовое выражение колеблемости признака для более глубокого понимания сущности изучаемых явлений

Задача статистики заключается в том, чтобы дать числовое выражение колеблемости признака для более глубокого понимания сущности изучаемых явлений. Для этого в статистике рассчитываются следующие показатели вариации:

- размах вариации (R);

- среднее линейное отклонение (Л);

- дисперсия (σ²);

- среднее квадратическое отклонение (σ),

Кроме них используют относительный показатель вариации – коэффициент вариации (V).

R вычисляется по формуле:

R=Хmaх – Хmin,

Xmaх (Хmin) - самое большое (малое) значение, принимаемое единицей совокупности.

Чем больше размах вариации, тем менее однородна совокупность по своему составу, по изучаемому признаку и тем менее надежна средняя. Этот показатель является очень приблизительным, т.к. учитывает лишь значения крайних единиц совокупности. Поэтому его применяют редко, лишь в тех случаях, когда особые значения имеют либо наибольшее, либо наименьшее значения варианты.

Стремление составить показатель вариации, который отражал бы все значения вариант, приводит к среднему линейному отклонению - это средняя арифметическая из абсолютных значении отклонений вариант от их средней арифметической. Применяется в двух формах:

Простой 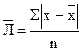и взвешенной .

Недостатком этого показателя является то, что он не учитывает знаки отклонений.

Чтобы усилить различия в величинах отклонений, эти отклонения возводятся в квадрат, тогда отклонения меньше 1 уменьшаются, а больше 1- увеличиваются и вводят новый показатель вариации- средний квадрат отклонения вариант от их средней арифметической или дисперсию (σ²). Используются в двух формах:

- простой: и - взвешенной:

Среднее квадратическое отклонение (σ) также как и дисперсия, измеряет абсолютный размер колеблемости признака, но измеряется в тех же единицах, что и варианта. Она рассчитывается по формуле:

.

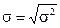Коэффициент вариации – отношение линейного или среднего квадратического отклонения к средней арифметической.

.

Принято считать, что если V>40%, то это свидетельствуют о большой колеблемости признака в изучаемой совокупности. В этом случае среднее значение ненадежно, недостоверно и по нему нельзя судить о всей совокупности.

ПРИМЕР: В таблице приведены данные о выполнении плана норм выработки группами рабочих завода

Группы рабочих по уровню выполнения плана норм выработки, %(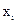)	Число рабочих, человек, ()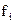
до 100
101-105
106-110
111-115
свыше 115
Итого

Определить:

1) обозначить варианты (признаки) и частоты;

2) средний уровень выполнения плана норм выработки;

3) размах вариации;

4) среднее линейное отклонение;

5) дисперсию признака;

6) среднее квадратическое отклонение;

7) коэффициент вариации;

8) линейный коэффициент вариации.

Решение:

* По условию необходимо рассчитать средний уровень выполнения плана норм выработки. Следовательно, в качестве вариант, т.е. значений осредняемого признака, принимаем уровни выполнения норм выработки. Варианты в статистике принято обозначать .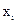

Частоты - это показатели, которые характеризуют число появления в исследуемой совокупности того или иного значения признака. Частоты принято обозначать 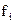. В нашем случае в качестве частот выступает число рабочих.

* Определим средний уровень выполнения плана норм выработки по формуле средней арифметической взвешенной, т.к. известны значения вариант осредняемого признака (x_i) и частоты (f_i) для каждой из вариант, показывающие их повторяемость. Причем частоты f_i¹const.

.

Сначала определим условные нижнюю и верхнюю границы первого и последнего интервала, принимая во внимание, что длина первого интервала принимается равной длине второго, а длина последнего - длине предыдущего интервала. Затем от интервального ряда перейдем к дискретному ряду, приняв в качестве вариант середины интервалов.

Расчеты следует проводить в таблице.

Таблица - Расчётная таблица

Группировка по уровню выполнения плана норм выработки, %	Количество рабочих,чел. (f)	Середина интервала (х)	xf
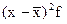
до 100				9,9375	-69,563	98,7539063	691,277344
101-105				4,9375	-83,938	24,3789063	414,441406
106-110				0,0625	1,8125	0,00390625	0,11328125
111-115				5,0625	121,5	25,6289063	615,09375
свыше 115				10,0625	30,1875	101,253906	303,761719
Итого				х		х	2024,6875

Расчет средних затрат времени будем производить по формуле средней арифметической взвешенной:

* Определим размах вариации (R) на основании данных исходного интервального ряда:

* Рассчитаем среднее линейное отклонение

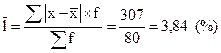
* Рассчитаем дисперсию и среднее квадратическое отклонение. Т.к. данные приведены в сгруппированном виде, то для расчета следует применить следующие формулы:

- дисперсия: , где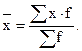

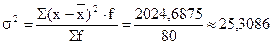
- среднее квадратическое отклонение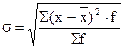

* коэффициент вариации

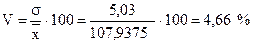
* линейный коэффициент вариации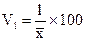

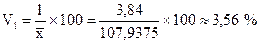
Вывод: произведенные расчеты показывают, что исследуемая совокупность является однородной (V=4,66 %<33 %).Следовательно все рассчитанные средние показатели надежны, т.е. достаточно верно характеризуют совокупность рабочих. Средний по совокупности рабочих процент выполнения норм выработки составляет около 107,94%.Все значения уровней выполнения норм выработки отклоняются от своего среднего значения в среднем на 3,84 процентных пунктов без учета знаков отклонения (3,56% в относительном выражении) и на 5,03 процентных пунктов (4,66%) с учетом знаков отклонения. Амплитуда изменения уровней выполнения норм составляет 24 процентных пунктов.

Дата добавления: 2014-01-07