
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика валового сбора зерновых культур в регионе за ряд лет
|
|
|
|
| Год | ||||||||||
| млн. тонн | 237,4 | 179,2 | 189,1 | 158,2 | 186,8 | 192,2 | 172,6 | 191,7 | 210,1 | 211,3 |
Изображение динамики валового сбора зерновых культур на координатной сетке с неразрывной шкалой значений, начинающихся от нуля, вряд ли целесообразно, так как 2/3 поля диаграммы остается неиспользованным и ничего не дает для выразительности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикального нуля, то есть шкала значений разрывается недалеко от нулевой линии и на диаграмму попадает лишь часть возможного поля графика. Это не приводит к искажениям в изображении динамики явления и процесс его изменения рисуется диаграммой более четко (рис. 5.15).
млн. тонн

 240
240
 |
 230
230
 220
220




 210
210
 200
200
 |  | ||
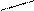
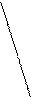




 190
190
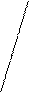 |

 180
180
 |
 170
170

 160
160










 0
0
год
Рис. 5.15. Динамика валового сбора зерновых культур в регионе.
 Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя в разных странах. Примером графического изображения сразу нескольких показателей может служить рис. 4.16.
Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя в разных странах. Примером графического изображения сразу нескольких показателей может служить рис. 4.16.




 115 млн. тонн
115 млн. тонн



 113 - готовый прокат
113 - готовый прокат




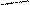

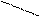




 111 - чугун
111 - чугун
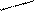



 109
109
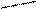
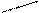






 107
107

 105
105




 103
103











 0
0
год
Рис. 5.16. Динамика производства чугуна и готового проката в регионе.
Линейные диаграммы с равномерной шкалой имеют один недостаток, снижающий их познавательную ценность. Этот недостаток заключается в том, что равномерная шкала позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателей на протяжении исследуемого периода. Однако при изучении динамики важно знать относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их изменения. Именно относительные изменения экономических показателей в динамике искажаются при изображении их на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных координатах теряет всякую наглядность и даже становится невозможным изображение рядов динамики с резко изменяющимися уровнями, которые обычно имеют место в динамических рядах за длительный период времени.
В этих случаях следует отказаться от равномерной шкалы и положить в основу графика полулогарифмическую систему.
Полулогарифмической сеткой называется сетка, в которой на одной оси нанесен линейный масштаб, а на другой логарифмический. В данном случае логарифмический масштаб наносится на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (годам, кварталам, месяцам, дням и прочее). Техника построения логарифмической шкалы следующая (рис. 5.17): необходимо найти логарифмы исходных чисел; начертить ординату и разделить на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например (0,000; 0,3010; 0,4771; 0,6021;...; 1,000, что дает 1, 2, 3, 4..., 10). Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате. Логарифмический масштаб лучше понять на примере.
Допустим, нам надо изобразить на графике динамику производства электроэнергии в регионе за ряд лет, за эти годы оно возросло в9,1 раза. С этой целью находим логарифмы для каждого уровня ряда (см. таблицу 5.3.)
Таблица 5.3.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 574; Нарушение авторских прав?; Мы поможем в написании вашей работы!