Основные характеристики системы массового обслуживания

Классификация и обозначение СМО.

Основные понятия и определения.

Тема 7. ЭММ систем массового обслуживания.

Система массового обслуживания (СМО) – это совокупность приборов, каналов, станков, линий обслуживания, на которые в случайные или детерминированные моменты времени поступают заявки на обслуживание. Например, коммутаторы телефонных станций, супермаркет, парикмахерские.

Оптимизация и оценка эффективности СМО состоит в нахождении средних суммарных затрат на обслуживание каждой заявки и нахождение средних суммарных потерь от заявок не обслуженных.

СМО состоит из определенного числа обслуживающих каналов и предназначена для выполнения заявок с разным характером распределения момента времени на обслуживание.

Моделирование СМО предполагает:

1) построение ЭММ, связывающих параметры СМО (число каналов, их производительность и т.п.) с показателями эффективности;

2) оптимизацию данных показателей с целью получения максимальной эффективности.

По ряду признаков СМО делятся на:

1. СМО: - с очередями;

- с отказами заявок (очереди);

2. СМО с очередью: - в порядке очереди;

- в случайном порядке;

- обслуживание с приоритетом (абсолютным или относительным);

3. СМО с многофазным обслуживанием;

4. СМО: - закрытые (замкнутые) – поток заявок генерируется самой системой;

- открытые – характер потока заявок не зависит от состояния СМО;

5. СМО: - одноканальные;

- многоканальные.

Обозначения СМО.

Для сокращения записи и характеристик СМО принята общемировая система записи по формату Кендола.

(a ç b ç c ç): (d çe çf)

a –характеризует закон распределения заявок входного потока;

b - характеризует закон распределения интервалов выполнения заявок на обслуживание;

c - характеризует количество каналов обслуживания;

d - характеризует дисциплину очереди;

e - характеризует максимальное количество требований (заявок) на обслуживание (е в очереди + е в обслуживании);

f – максимальный объем источника (генератора) заявок.

Пример.

GI çG ç N

GI - данная позиция характеризует, что момент заявок, поступающих на обслуживание, распределен по случайному закону с функцией распределения F(x) с математическим ожиданием .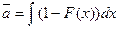

F(x) – любой закон распределения;

G - данная позиция характеризует моменты распределения (временные интервалы) обслуживания заявок с любой функцией распределения H(x) и со средним временем обслуживания .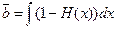

(M₁ ç M₂ ç N): - характеризует, что поток заявок, поступающих на обслуживание как входящий поток, подчиняется закону Пуассона с функцией распределения ,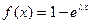

l - интенсивность потока заявок;

M₁ – простейший поток заявок;

N – количество мест по обслуживанию заявок;

M₂ – характеризует поток обслуживания и распределения времени обслуживания также по простейшему Пуассоновскому закону с функцией распределения ,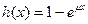

m - характеризует интенсивность потока обслуживания.

Простейший поток обладает тремя свойствами:

1) стационарностью;

2) безпоследействия;

3) ординарностью.

Стационарность – это когда вероятность попадания того или иного числа заявок на интервал времени длиной t зависит от длины этого интервала и не зависит от того, где этот интервал расположен на оси времени.

Поток безпоследействия – когда для любых не перекрывающихся участков времени число заявок, попадающих на один из участков, не зависит от числа заявок, попадающих на другой участок.

Ординарность – это когда вероятность попадания на участок t двух или более заявок пренебрежимо мала по сравнению с вероятностью попадания одной заявки.

Поток, обладающий вышеназванными тремя свойствами, называется простейшим (стационарным, Пуассоновским) потоком.

Эрланговский поток – «просеянный» простейший поток с коэффициентом k = (2;3;4...), то есть когда обслуживается каждая 2,3,...,k заявка.

E_l êE_m êN_M – эрланговский входной поток заявок E_l и эрланговский закон обслуживания E_m.

Характеристиками, принятыми для СМО, являются:

1) вероятность потери заявок

Р_отказа = Р_потерь

2) вероятность занятости k каналов

Р_к

3) среднее число занятых каналов

4) коэффициент простоя каналов

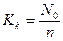
N₀ – незанятых каналов,

n – всего каналов.

5) средняя длина очереди

6) среднее число требований, находящихся на обслуживании

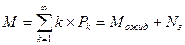
Эффективность СМО можно определить, используя следующую методику:

(*) Е^СМО =

q_ожид –потери в результате ожидания 1 заявки в единицу времени;

q_nk – стоимость простоя одного канала в единицу времени;

q_k - стоимость эксплуатации одного канала в единицу времени;

(*) – показывает один из возможных подходов к оценке эффективности СМО. Как правило для высокоточных оценок эффективности используются имитационные модели.

Дата добавления: 2014-01-07