Метод наименьших квадратов (МНК)

Суть данного метода заключается в том, что квадрат суммы разностей между фактическим значением результативного признака и его теоретическим значением сводится к минимуму.

*

F = å (у_факт – у_теор)² Þ min

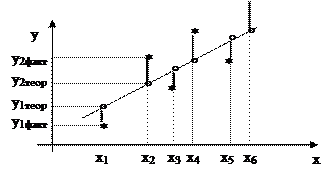* - у_факт (эмпирическое)

Чтобы найти параметры a₀, a₁, a₂, необходимо в формулу (1) подставить у _теор, то есть ту аналитическую зависимость, которой будем сглаживать (аппроксимировать) статистический материал. Как известно из математики для нахождения минимума функции нужно взять частные производные по анализируемым параметрам, то есть... и приравнять данное выражение к нулю. Получим систему нормальных уравнений, из которых найдем заданные коэффициенты.

F = å (у_факт – a₀ – a₁x_факт)² Þ min

у_расч = a₀ + a₁x_факт

(*)

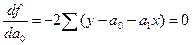
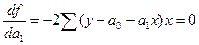
преобразовав уравнение (*), получим систему нормальных уравнений:

(**)

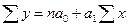
решением системы (**) будут:

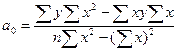
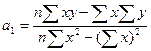
Рассчитав коэффициенты a₀, a₁, можно синтезировать модель:

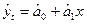(оценки коэффициентов a₀, a₁)

Аналогичным образом используя МНК, можно получить коэффициенты для остальных функций, используемых при аппроксимации.

Если в качестве факторного признака х используется время t, то такой ряд называется динамическим (временным) рядом. При применении специального подхода при обозначении факторного признака t, когда сумма времени t будет равна 0, выражения для коэффициентов a₀, a₁, a₂ – будут проще.

t_i, åt = 0

-2	-1

При таком подходе формулы коэффициентов a₀, a₁ значительно упрощаются:

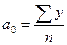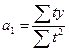, (для линейной функции)

Аналогично определяем коэффициенты для других функций:

y_t =a₀ +a₁t +a₂t² (парабола)

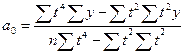
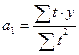
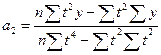
y =a₀ a₁^t (показательная функция)

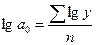
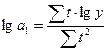
Для того, чтобы убедится, что полученные коэффициенты являются типичными, используют метод оценки с помощью распределения Стьюдента (критерий Стьюдента). Находят:

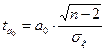
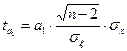
s - среднее квадратичное отклонение;

s² – дисперсия

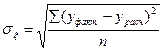- остаточная дисперсия

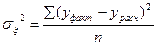
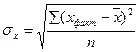
Отделив t_a0, t_a1 и сравнив с t_{табличное}, можно сделать вывод, что если t_a0 > t_{табличное} и

t_a1 > t_{табличное} (t_a0 >t_{табличное}< t_a1), то параметры а₀ и а₁ – стандартно типичны (обладают оценкой несмещенной, эффективной).

Получив синтезированные модели по функциям 1-5 срвнивают остаточную диперсию и по минимальности остаточной диперсии выбирают функцию для аппроксимации (сглаживания).

Для оценки прогноза используют обычно не дискретные (точечные) значения результативного признака, а рассчитанный интервал.

Y_{прогнозное} = y_теор ± t_a s_x*

a - коэффициент доверия, обычно выбирается 0,05 и вероятность Р=0,95.

t_a - находится по таблице Стьюдента (t_a = 4,3).

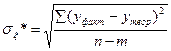
s_x* - скорректированное среднее квадратичное отклонение с учетом степеней свободы n - m, где

m - число параметров нашей синтезируемой модели;

n - объем выборки.

Для y =a₀ +a₁x, m = 2

Дата добавления: 2014-01-07