Практические вопросы дискретизации реальных сигналов

Сообщения, передаваемые по каналам связи (речь, музыка, телевизионный сигнал, телеметрические данные и т.д.), на практике являются функциями с ограниченным спектром. Например, верхняя частота спектра F_m примерно равна: для речи - 3,5 кГц, для музыки - 10 - 12 кГц (удовлетворительное воспроизведение), для телевизионных сигналов - 6 МГц.

Некоторая некорректность состоит в том, что теорема отсчетов доказана для функций Х(t), заданных на неограниченном интервале t Î (-¥, ¥). Соответственно отсчеты { Х(iDt), i = 0, ±1, ±2,..} представляют собой бесконечную последовательность. Однако в реальных условиях сообщения Х(t) имеют начало и конец, а следовательно, конечную длительность T< ¥. Условия финитности спектра и конечной длительности сообщения, строго говоря, несовместимы. Спектр функции с конечной длительностью теоретически имеет значения, отличные от нуля, при любых значениях частоты FÎ (-¥, ¥). Тогда при любом выборе шага дискретизации Dt соседние боковые полосы спектра (см. рис.1.4) перекрываются, и на выходе идеального фильтра нижних частот с частотой среза F = 1/2 Dt будет восстановлен сигнал Х^*(t), не полностью совпадающий с исходным сигналом Х(t). Во-первых, отсекаются частотные составляющие спектра с |f| >F. Во-вторых, в полосу пропускания фильтра попадают "хвосты" периодического продолжения спектра.

Вместе с тем всегда можно задать шаг дискретизации Dt (или верхнюю частоту спектра F_m =1/2 Dt) так, чтобы энергия Э_D, сосредоточенная в отсекаемых "хвостах" спектра (на частотах f >1/2 Dt), была пренебрежимо мала по сравнению с энергией всего сигнала Э_x. Ошибка восстановления сигнала Х^*(t) на выходе фильтра зависит от отношения Э_D /Э_x и может быть выбором Dt (или F=1/2 Dt) сделана меньше любой заданной величины. Совершенно очевидно, что если искажения сообщений, обусловленные временной дискретизацией, будут значительно меньше искажений, вызванных помехами в канале связи и допустимых техническими условиями для данной системы передачи информации, то такие искажения существенного значения не имеют и могут не учитываться.

Таким образом, приближенно можно принять, что реальные сообщения имеют конечную длительность T и одновременно их спектры ограничены по частоте величиной F_m. При этом бесконечный ряд Котельникова (1.17) преобразуется в конечный с числом ненулевых отсчетов n, примерно равным отношению длительности сообщения к интервалу дискретности:

(1.18)

Основные формулы теоремы отсчетов для сигналов, отличных от нуля на конечном интервале tÎ (0, T), принимают вид:

(1.19)

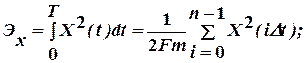(1.20)

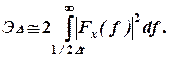(1.21)

Наконец, когда сигнал { X(t), tÎ(0, T) } задан конечным числом отсчетов X(0), X(Dt),.., x(kDt), в формулах (1.17) - (1.19) в отличие от соответствующих точных формул следовало бы писать знак приближенного равенства (@). Однако обычно этого не делают.

Еще одним приближением, которое не может быть выполнено в действительности, является предположение об "идеальности" амплитудно-частотной характеристики восстанавливающего фильтра H(f). Дело в том, что фильтр с идеально прямоугольной АЧХ имеет ИПХ бесконечной длительности и не может быть реализован на практике. Фильтры же с конечной ИПХ имеют теоретически бесконечную полосу. Нетрудно показать, что влияние конечной длительности ИПХ восстанавливающего фильтра на сигнал Х^*(t) имеет тот же характер, что и ограниченность интервала наблюдения функции Х(t).

Следовательно, для фильтра НЧ с заданной АЧХ всегда можно выбрать шаг дискретизации Dt таким, чтобы энергия Э_D, просачивающаяся через "хвосты" его амплитудно-частотной характеристики (на частотах f >1/2 Dt), была пренебрежимо мала по сравнению с энергией всего сигнала Э_x. В связи с этим на практике шаг дискретизации реальных сообщений Х(t) делают несколько меньшим, а частоту дискретизации, соответственно, – несколько большей (по крайней мере, на 30 - 50 %), нежели предписывает теорема Котельникова.

Дата добавления: 2014-01-07