Квантование сообщений. Ошибки квантования

Итак, показано, что передачу практически любых сообщений λ(t) ({λ(x,y)}) можно свести к передаче их отсчетов, или чисел λ_i = λ (i Dt), следующих друг за другом с интервалом дискретности Dt £ 1/2F_m (Δx ≤ 1/2f_x, Δy ≤ 1/2f_y). Тем самым непрерывное (бесконечное) множество возможных значений сообщения λ(t) заменяется конечным числом его дискретных значений { λ (i Dt)}. Однако сами эти числа имеют непрерывную шкалу уровней (значений), то есть принадлежат опять же континуальному множеству. Для абсолютно точного представления таких чисел, к примеру, в десятичной (или двоичной) форме, необходимо теоретически бесконечное число разрядов. Вместе с тем на практике нет необходимости в абсолютно точном представлении значений λ_i, как и любых чисел вообще.

Во-первых, сами источники сообщений обладают ограниченным динамическим диапазоном и вырабатывают исходные сообщения с определенным уровнем искажений и ошибок. Этот уровень может быть большим или меньшим, но абсолютной точности воспроизведения достичь невозможно.

Во-вторых, передача сообщений по каналам связи всегда производится в присутствии различного рода помех. Поэтому принятое (воспроизведенное) сообщение (оценка сообщения l^*(t) или L ^*) всегда в определенной степени отличается от переданного, то есть на практике невозможна абсолютно точная передача сообщений при наличии помех в канале связи.

Наконец, сообщения передаются для их восприятия и использования получателем. Получатели же информации - органы чувств человека, исполнительные механизмы и т.д. - также обладают конечной разрешающей способностью, то есть не замечают незначительной разницы между абсолютно точным и приближенным значениями воспроизводимого сообщения. Порог чувствительности к искажениям также может быть различным, но он всегда есть.

С учетом этих замечаний процедуру дискретизации сообщений можно продолжить, а именно подвергнуть отсчеты λ_i квантованию.

Процесс квантования состоит в замене непрерывного множества значений отсчетов l_i Î (l_min , l_max ) дискретным множеством { l₍₁₎,...,l_(m) } из алфавитаA { λ_i }. Тем самым точные значения чисел l_i заменяются их приблизительными (округленными до ближайшего разрешенного уровня) значениями. Интервал между соседними разрешенными уровнями l_i, или уровнями квантования, D = l_(i+1) - l_(i) называется шагом квантования.

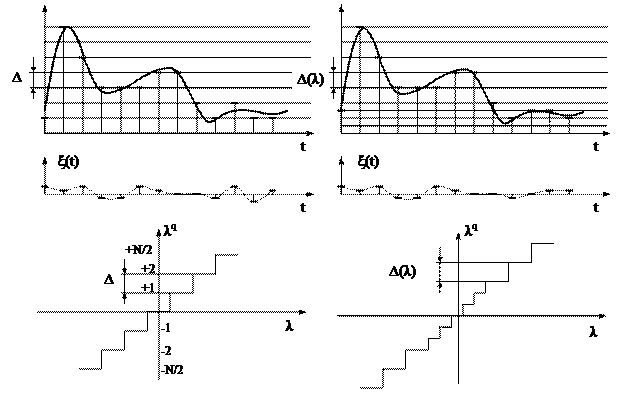Рис. 1.9 Рис. 1.10

Различают равномерное и неравномерное квантование. В большинстве случаев применяется и далее подробно рассматривается равномерное квантование (рис. 1.9), при котором шаг квантования постоянный: D = λ_i - λ_i-1 = = const; однако иногда определенное преимущество дает неравномерное квантование, при котором шаг квантования D_i разный для различных λ_i (рис. 1.10).

Квантование приводит к искажению сообщений. Если квантованное сообщение, полученное в результате квантования отсчета l_i = l(iΔ t ), обозна-чить как λ_iq, то

(1.25)

где x _i - разность между квантованным сообщением (ближайшим разрешенным уровнем) λ_iq и истинным значением элементарного сообщения l_i, называемая ошибкой квантования, или шумом квантования. Шум квантования оказывает на процесс передачи информации по существу такое же влияние, как и помехи в канале связи. Помехи, так же как и квантование, приводят к тому, что оценки λ^*_i, получаемые на приемной стороне системы связи, отличаются на некоторую величину от истинного значения l_i.

Поскольку квантование сообщений приводит к появлению ошибок и потере некоторой части информации, можно определить цену таких потерь d( l, λ_q) и среднюю величину ошибки, обусловленной квантованием:

(1.26)

Чаще всего в качестве функции потерь (цены потерь) используется квадратичная функция вида

(1.27)

В этом случае мерой ошибок квантования служит дисперсия этих ошибок. Для равномерного N -уровневого квантования с шагом D дисперсия ошибок квантования определяется следующим образом:

. (1.28)

Абсолютное значение ошибки квантования не превосходит половины шага квантования D/2, и тогда при достаточно большом числе уровней квантования N и малой величине D плотность распределения вероятностей ошибок квантования f( x _i) можно считать равномерной на интервале + D/2 … - D/2:

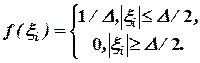(1.29)

В результате величина ошибки квантования D(q) = σ_q² определится соотношением

(1.30)

и соответствующим выбором шага квантования D может быть сделана сколь угодно малой или сведена к любой наперед заданной величине.

Относительно требуемой точности передачи отсчетов сообщений можно высказать те же соображения, что и для ошибок временной дискретизации: шумы квантования или искажения, обусловленные квантованием, не имеют существенного значения, если эти искажения меньше ошибок, обусловленных помехами и допустимых техническими условиями.

Так, например, при передаче речи и музыки искажения практически не заметны, если все отсчеты случайным образом изменить на 0,1…1%, при передаче изображений - на 1% и т.д. Даже профессиональный эксперт не может заметить искажений в музыкальном произведении, если квантование производится с точностью лучше 0,001% (число уровней квантования N > 100000, точность представления отсчетов - 16…17 двоичных разрядов). Число уровней квантования сообщений в телеметрических системах зависит от требуемой точности воспроизведения информации, а также от точности датчиков, осуществляющих сбор этой информации. При этом превышение при квантовании достижимой датчиками или требуемой точности нецелесообразно из-за увеличения сложности аппаратуры и затрат на передачу. Более того, при передаче по каналу связи с помехами могут возникать ситуации, когда качество воспроизведения оценки сообщения λ^*_i при более грубом его квантовании на передающей стороне оказывается значительно лучшим, чем для точного квантования. На этом достаточно неочевидном, но вытекающем из общей теории передачи информации явлении в дальнейшем более подробно остановимся.

Таким образом, показано, что передачу практически любых сообщений λ(t) ({λ(x,y)}) с любой наперед заданной точностью можно свести к передаче целых чисел λ_iq = λ_q (i Dt), следующих друг за другом с интервалом дискретности Dt £ 1/2F_m (Δx ≤ 1/2f_x max, Δy ≤ 1/2f_y max). Тем самым непрерывное (бесконечное) множество возможных значений сообщения λ(t) ({λ(x,y)}) заменяется конечным множеством целых чисел из алфавита A { λ_{i q} }, (i = 1,2…N). Иными словами, теперь можно работать с сигналами, как с числами, а это позволяет применять для их обработки и анализа цифровые алгоритмы любой степени сложности, практически нереализуемые в аналоговой форме, использовать в системах передачи информации цифровые методы и современные цифровые интегральные технологии и т.д.

Итак, мы выяснили, что в радиотехнических системах носителями или переносчиками информации являются электрические сигналы, формируемые источниками этой информации. Даже в тех случаях, когда первичная информация носит неэлектрическую природу (речь, музыка, изображения, тексты, пакеты данных и т.д.), она в конечном итоге преобразуется в электрические сигналы и далее сохраняется или передается по каналам связи. Эти сигналы обычно носят непрерывный характер, то есть определены для любого момента времени или в бесконечном числе точек своего существования. Гораздо удобнее иметь дело с данными, имеющими конечный размер, – например, с массивами чисел конечного размера и ограниченной разрядности. Рассмотренная выше теорема дискретизации дает такую возможность.

Дата добавления: 2014-01-07