Кодирование с использованием циклических кодов

Циклические коды

Частным и наиболее широко распространенным классом полиномиальных кодов являются циклические коды.

Линейный (n,k)-код называется циклическим, если в результате циклического сдвига кодового слова получается другое кодовое слово данного кода. Другими словами, если U = (U₀, U₁,...U_{n- 1}) является кодовым словом, то и V = (U_{n- 1}, U₀, U₁,...U_{n- 2}), полученное циклическим сдвигом U, является кодовым словом данного кода.

Циклические коды привлекательны по двум причинам.

Во-первых, операции кодирования и вычисления синдрома для них выполняются очень просто с использованием сдвиговых регистров.

Во-вторых, этим кодам присуща алгебраическая структура, и можно найти более простые и эффективные способы их декодирования.

Основные свойства циклических кодов:

1. В циклическом (n,k)-коде каждый ненулевой полином должен иметь степень, по крайней мере (n-k), но не более n-1.

g(x)=1 + g₁ × x + g₂ × x² +...+ g_n-k-1 × x^n-k-1 + x^n-k, (3.60)

2. Существует только один кодовый полином g(x) степени (n-k)

вида
называемый порождающим полиномом кода.

3. Каждый кодовый полином U(x) является кратным g(x), то есть

U(x)= m(x) × g(x). (3.61)

Предположим, надо закодировать некоторую информационную последовательность

m = (m₀, m₁, m₂... m_{k- 1}). (3.62)

Соответствующий ей полином выглядит следующим образом:

m(x)= m₀ + m₁ × x + m₂ × x² +...+m_{k- 1} × x^k-1. (3.63)

Умножив m(x) на x^n-k:

x^n-k × m(x)= m₀ × x^n-k + m₁ × x^n-k+1 +...+m_{k- 1} × x^n-1, (3.64)

получим полином степени n-1 или меньшей.

Воспользовавшись теоремой о делении полиномов, можно записать

x^n-k × m(x) = q(x) × g(x) + r(x), (3.65)

где q(x) и r(x) — частное и остаток от деления полинома x^n-k × m(x) на порождающий полином g(x).

Поскольку степень g(x) равна (n-k), то степень r(x) должна быть (n-k-1) или меньше, а сам полином r(x) будет иметь вид

r(x)= r₀ + r₁ × x + r₂ × x² +...+ r_{n- k- 1} × x^n-k-1 . (3.66)

С учетом правил арифметики в GF(2) данное выражение можно переписать следующим образом:

r(x) + x^n-k × m(x) = q(x)× g(x), (3.67)

откуда видно, что полином r(x)+x^n-k × m(x) является кратным g(x) и имеет степень n-1 или меньшую. Следовательно, полином r(x)+x^n-k × m(x) - это кодовый полином, соответствующий кодируемой информационной последовательности m(x).

Раскрыв последнее выражение, получим

r(x)+m(x)× x^n-k =r₀ +r₁ x +r₂ x²..+r_{n- k-1} x^n-k-1 + m₀ x^n-k + m₁ × x^n-k+1 +..+ m_k-1 x^n-1,

что соответствует кодовому слову

U=	(r0, r1 ... rn- k-1 ,	m0, m1 ... mk-1),
	проверочные символы	информационные символы

Таким образом, кодовое слово состоит из неизменной информационной части m, перед которой расположено (n-k) проверочных символов. Проверочные символы являются коэффициентами полинома r(x), то есть остатка от деления m(x) × x^n-k на порождающий полином g(x).

Чтобы полученный результат был понятнее, напомним, что умножению некоторого двоичного полинома на x^n-k соответствует сдвиг двоичной последовательности m = (m₀, m₁ ... m_k-1) на n-k разрядов вправо.

Рассмотрим пример. С использованием кода, задаваемого порождающим полиномом g(x) = 1 + x + x³, закодируем произвольную последовательность, например m = (0111).

Последовательности m =(0111) соответствует полином m (x)=x+ x² + x³.

Умножим m(x) на x^n-k:

m(x) × x^n-k =m(x) × x³ =(x + x² + x³) × x³ = x⁴ + x⁵ + x⁶ . (3.68)

Разделим m(x) × x^n-k на порождающий полином g(x):

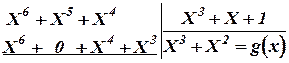X⁵ + 0 + X³ X⁵ + 0 + X³ +X² X²=r(x). (3.69)

Таким образом, кодовый полином, соответствующий информационной последовательности m = (0111), будет иметь следующий вид:

U(x) = 0*X⁰ + 0*X¹ + 1*X² + 0*X³ + 1*X⁴ + 1*X⁵ + 1*X⁶, (3.70)

а соответствующее кодовое слово U = (0010111).

Итак, циклический (n,k)- код k- разрядной информационной последовательности m = (m₀, m₁ ... m_k-1) получают следующим образом:

- информационную последовательность m умножают на x^n-k, то есть сдвигают вправо на n-k разрядов;

- полином полученной последовательности делят на порождающий полином кода g(x);

- полученный остаток от деления m(x) × x^n-k на g(x) прибавляют к m(x) × x^n-k, то есть записывают в младших n-k разрядах кода.

Алгоритм кодирования, основанный на делении полиномов, можно реализовать, используя схему деления. Она представляет собой регистр сдвига, в котором цепи обратной связи замкнуты в соответствии c коэффициентами порождающего полинома g(x) (рис. 1.10).

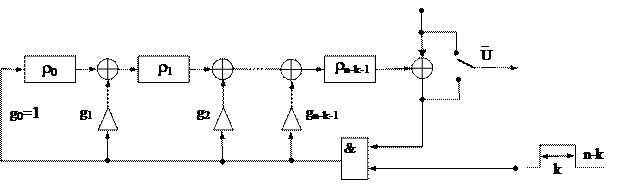Рис. 3.10

Кодирование в схеме рис. 3.10 выполняется следующим образом:

- k символов информационной последовательности m через переключатель П, находящийся в верхнем положении, один за другим передаются в канал и одновременно с этим через открытую схему И записываются в регистр проверочных символов, в котором благодаря наличию цепей обратной связи g₀ ... g_n-k-1 формируется остаток от деления x^n-k × m(x) на g(x) — проверочные символы;

- начиная с ( k+1)- го такта переключатель переводится в нижнее положение, и из сдвигового регистра выводятся (n-k) проверочных символов; цепь обратной связи при этом разомкнута (схема И - закрыта).

Для циклического (7,4)- кода Хемминга (а этот код обладает свойством цикличности), используемого в качестве примера и имеющего порождающий полином g(x) = 1 + x + x³, схема кодирования выглядит следующим образом (рис. 3.11):

Рис. 3.11

В этой схеме, в отличие от обобщенной схемы кодера рис. 1.10, отсутствуют элементы в цепях, где значения коэффициентов обратной связи g_i равны нулю, там же, где коэффициенты передачи g_i равны единице, цепь просто замкнута.

На примере этого же кода и соответствующего ему кодера рассмотрим в динамике процесс кодирования произвольной последовательности m.

Пусть m = (1001). Тогда последовательность состояний ячеек сдвигового регистра с обратными связями в процессе кодирования будет определяться табл. 3.4.

Таблица 3.4

Номер такта	Положение переключателя	Уровень разрешения	Вход m	Состояние ячейки регистра	Выход
P0	P1	P2	U
0 1 2 3 4 5 6 7	­ ­ ­ ­ ¯ ¯ ¯ ¯	1 1 1 1 0 0 0 0	1 0 0 1 0 0 0 0	1 0 1 0 0	1 1 1 1 0 0	0 1 1 1 1 0 0	1 0 0 1 1 1 0

Еще одним важным свойством циклического (n,k)- кода, вытекающим из теоремы о существовании циклических кодов, является то, что его порождающий полином делит без остатка двучлен xⁿ +1, то есть

xⁿ + 1 = g(x)× h(x) + 0. (3.71)

Полином h(x) — частное от деления xⁿ +1 на g(x) -называется проверочным полиномом.

Поскольку h(x) однозначно связан с g(x), он также определяет код. Следовательно, с помощью проверочного полинома h(x) тоже можно производить кодирование. Схема кодирования на основании проверочного полинома h(x) приведена на рис. 3.12.

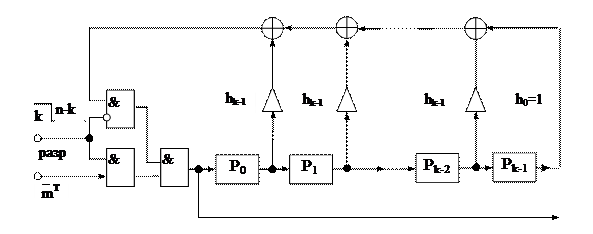
Рис. 3.12

Процедура кодирования на основании h(x) выглядит следующим образом:

1. На входе "Разрешение" устанавливается 1, при этом открывается нижняя схема И и закрывается верхняя.

2. Сообщение m последовательно записывается в k - разрядный сдвиговый регистр и одновременно с этим передается в канал.

3. По окончании ввода k информационных символов на входе "Разрешение" устанавливается 0, замыкая через верхнюю схему И цепь обратной связи.

4. Производится (n-k) сдвигов, при этом формируются и выдаются в канал (n-k) проверочных символов.

Для циклического (7,4) -кода с порождающим полиномом g(x)= 1+ x + x³ проверочный полином h(x) имеет вид

(3.72)

С учетом этого схема кодирования на основании полинома h(x) для (7,4)- кода выглядит следующим образом (рис. 3.13):

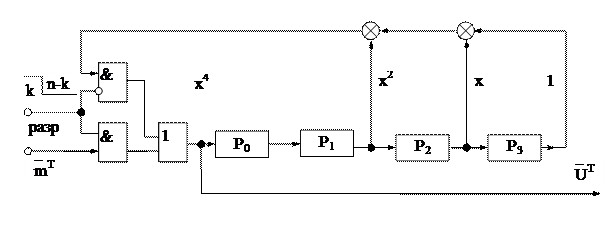
Рис. 3.13

Дата добавления: 2014-01-07