Вычисление синдрома и исправление ошибок в циклических кодах

Вычисление синдрома для циклических кодов является довольно простой процедурой.

Пусть U(x) и r(х) ‑ полиномы, соответствующие переданному кодовому слову и принятой последовательности.

Разделив r(x) на g(x), получим

r(x) = q(x)× g(x) + s(x), (3.73)

где - q(x) — частное от деления, s(x) — остаток от деления.

Если r(x) является кодовым полиномом, то он делится на g(x) без остатка, то есть s(x) = 0.

Следовательно, s(x) ¹ 0 является условием наличия ошибки в принятой последовательности, то есть синдромом принятой последовательности.

Синдром s(x) имеет в общем случае вид

S(x) = S₀ + S₁ × x +... + S_{n- k-1} × x^n-k-1. (3.74)

Очевидно, что схема вычисления синдрома является схемой деления, подобной схемам кодирования рис. 3.10 или 3.11.

При наличии в принятой последовательности r хотя бы одной ошибки вектор синдрома S будет иметь, по крайней мере, один нулевой элемент, при этом факт наличия ошибки легко обнаружить, объединив по ИЛИ выходы всех ячеек регистра синдрома.

Покажем, что синдромный многочлен S(x) однозначно связан с многочленом ошибки e(x), а значит, с его помощью можно не только обнаруживать, но и локализовать ошибку в принятой последовательности.

Пусть

e(x) = e₀ + e₁ × x + e₂ × x² +... + e_n-1 × x ^n-1 (3.75)

— полином вектора ошибки.

Тогда полином принятой последовательности

r(x) = U(x) + e(x). (3.76)

Прибавим в этом выражении слева и справа U(x), а также учтем, что

r(x) = q(x)× g(x) + S(x), U(x) = m(x)× g(x), (3.77)

тогда

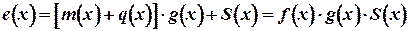, (3.78)

то есть синдромный полином S(x) есть остаток от деления полинома ошибки e(x) на порождающий полином g(x).

Отсюда следует, что по синдрому S(x) можно однозначно определить вектор ошибки e(x), а следовательно, исправить эту ошибку.

На рис. 3.14 приведена схема синдромного декодера с исправлением однократной ошибки для циклического (7,4)- кода. По своей структуре она подобна схеме, приведенной на рис. 3.6, с той лишь разницей, что вычисление синдрома принятой последовательности производится здесь не умножением на проверочную матрицу, а делением на порождающий полином. При этом она сохраняет и недостаток, присущий всем синдромным декодерам: необходимость иметь запоминающее устройство, ставящее в соответствие множеству возможных синдромов S множество векторов ошибок e. Цикличность структуры кода в этом случае не учитывается.

Рис. 3.14

Дата добавления: 2014-01-07