Надежность элемента, работающего до первого отказа

Напомним, что под элементом, работающим до первого отказа, понимается невосстанавливаемый элемент, которой после выхода из строя не может быть отремонтирован. Пусть в момент t = 0 элемент начал работу, а в момент t = t произошел отказ. Тогда t будет время жизни элемента, его истинный ресурс.

Если t случайная величина и известен ее закон распределения, то вероятность отказа аналогичных элементов определится из формулы

Q (t) =P { t < t }, (3.2)

где P { t < t } — вероятность отказа элемента до момента t, определенная на множестве элементов, срок жизни которых менее рассматриваемого момента.

Предполагается, что Q (t) непрерывна, и существует непрерывная плотность вероятности отказа, которая выразится первой производной

q (t)= Q '(t) (3.3)

где q (t) — плотность вероятности отказа.

Отметим, что предположение t случайной величиной является серьезным допущением, которое на практике, очевидно, не всегда справедливо.

Функция Q (t) полностью определяет надежность элемента. Однако это определение является формальным и не отражает физической сущности старения. Наряду с функцией (3.2) применяется и другая функция

Р (t) = 1 -Q (t) =Р { t > t }. (3.4)

Формула (3.4) определяет среднюю вероятность безотказной работы за время t. Эту функцию чаще всего называют функцией надежности. Примерный вид функций надежности и ненадежности показан на рис. 3.2.

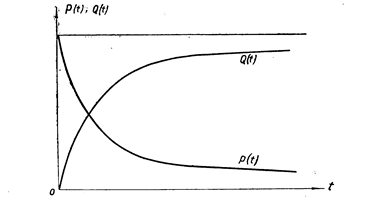
Рис. 3.2. Вид функций: надежности – P (t), и ненадежности – Q (t)

Функция монотонно убывает Р (0) = 1, Р (t) ® 0, при t ® ¥; Q = 0 и Q (t) ® 1 при t ® ¥.

Функцию Р (t) можно приближенно найти из опыта. На испытание ставится N элементов и испытывается в одинаковых условиях в течение времени t = t₀. Если к моменту t₀ не отказало п элементов, то по теореме Бореля

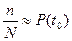при N ®¥

что позволяет с некоторым приближением считать

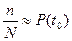(3.5)

Можно функцию Р (t) найти для всех значений t£ t ₀. Для этого при проведении испытаний необходимо отмечать истинное время отказов элементов. По моментам отказов можно определить функцию п (t), которая численно равна числу элементов, не отказавших к моменту t. В начальный момент (при t =0) п (t) =N, а в момент каждого отказа уменьшается на единицу.

Тогда формулу (3.5) можно записать следующим образом:

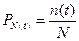(3.6)

Отношение (3.6) называется эмпирической функцией надежности. С ростом N эта функция равномерно приближается к Р (t) и для больших N

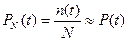(3.7)

Функцию Р (t) в общем случае нельзя экстраполировать за пределы участка испытания. Для оценки функции Р (t) требуется гораздо больший объем испытаний, чем для функции Р (t ₀) (при одинаковой точности). Поэтому часто эти функции не определяются, а надежность характеризуют числовыми величинами.

Важнейшей из них является среднее время безотказной работы, которая определяется как математическое ожидание случайной величины τ

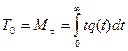(3.8)

После преобразования:

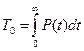(3.9)

Формула (3.9) показывает, что Т ₀ (среднее время безотказной работы) геометрически выражается площадью фигуры, ограниченной осями координат и кривой Р (t) (рис. 3.2).

Среднее время можно определить по результатам испытаний. Для этого, необходимо определить

(3.10)

где:

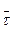- среднее время жизни элемента;

τ_1,2 - время жизни i -го элемента;

N – число элементов, подвергнутых испытанию.

Согласно закону больших чисел с вероятностью единица

`t® T ₀ при N ® ¥

при большом N

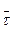» T ₀ (3.11)

К сожалению, подобные испытания неосуществимы, т.к. нельзя ждать, пока откажут все элементы (большая потеря времени). Поэтому можно оценить приближенно

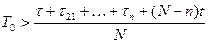(3.12)

n – число отказавших элементов;

T ₀ - среднее время безотказной работы;

t _i – время жизни элемента.

Этой оценкой можно пользоваться при n, близком к N.

Вкратце упомянем о некоторых других характеристиках надежности.

1. Дисперсия времени жизни.

Теоретическая формула

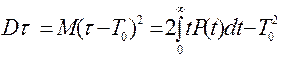(3.13)

Опытная формула

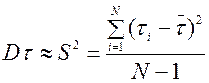(3.14)

где

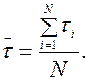
2. Среднее квадратичное отклонение.

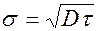(3.15)

Формула (3.15) дает среднее квадратичное отклонение времени от среднего Т ₀. Использование дисперсии как характеристики надежности целесообразно тогда, когда s< Т ₀, то есть случайное время t имеет небольшой относительный разброс.

В этом случае яркое представление о надежности дает график плотности q (t), который, как правило, имеет один максимум (рис. 3.3а).

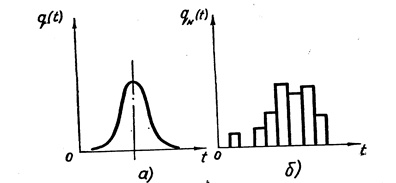
Рис. 3.3 Гистограммы плотности q (t): а) теоретическая: б) эмпирическая

Функция q (t) может быть определена из опыта. Участок оси разбивается на интервалы (рис. 3.3б).

Пусть поставлено на испытания N элементов и произошло n_k отказов на интервале [(k —1) h; kh ] k =1, 2, 3,...и т.д. (целое число).

Тогда эмпирическая функция плотности или гистограмма выразится ступенчатой линией, изображенной на рис. 3.3б. Высота каждой ступеньки определится по формуле

(3.16)

если

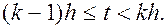
При большом объеме испытаний и достаточно малом h

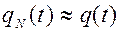(3.17)

Рассмотрим теперь важнейшую характеристику надежности, называемую интенсивностью отказа.

Интенсивность отказа является локальной характеристикой, определяющей надежность элемента в каждый момент времени. В общем виде она выражается формулой

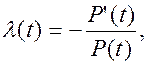(3.18)

где

l(t) – функция интенсивности отказа;

P ¢(t) – первая производная от функции надежности;

P (t) – функция надежности.

В теории вероятностей l(t) называют плотностью условной вероятности события в момент t при условии, что до этого момента событие не наступило.

Применительно к теории надежности l(t), это вероятность того, что элемент, проработавший безотказно до момента t, откажет в последующую единицу времени (при условии, что эта единица времени будет небольшой). Формула (3.18) разрешается относительно функции надежности

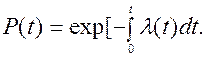(3.19)

Уравнение (3.19) является одним из основополагающих в стохастической теории надежности. Из него следует, что вероятность безотказной работы элемента на участке (t ₁; t ₂) будет равна

Функция интенсивности отказа может быть определена опытным путем по результатам испытаний.

Испытываются N элементов и регистрируются их отказы. Пусть n (t) -число элементов, не отказывающих к моменту t. Тогда при достаточно малом D t и достаточно большом N

где D n - число отказов на участке (t; t +D t);

n (t) – функция отказов, численно равная числу элементов, не отказавших к моменту t.

Итак, если D t достаточно мало, а D n при этом велико, то

(3.20)

По результатам статистических испытаний можно сказать (формула 3.20), что интенсивность отказа равна числу отказов, происшедших в единицу времени, отнесенному к числу не отказавших к данному моменту элементов.

Рассмотрим один пример.

На испытания ставятся 1000 элементов. В первый час отказывает 50 элементов. В последующие 100 часов отказывают 890 элементов, причем отказы следуют равномерно во времени. В следующий (после 100 часов) отказывают еще 20 элементов. Спрашивается: когда элемент имеет наивысшую надежность?

Абсолютные цифры не могут характеризовать этого явления. Очевидно, что наиболее надежный элемент имеет минимальную интенсивность отказов. По формуле (3.20)

а) За 1-й час

,

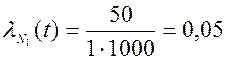б) за последующие 100 часов

,

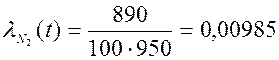в) за последний час испытаний

.

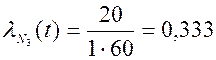Практически кривую интенсивности отказов можно построить по методике построения кривой q (t).

Для этого:

а) ось абсцисс (времени) разбивается на интервалы длительности h,

б) из испытаний определяется число отказов, попавших в каждый интервал h_k.

Если п_k число отказов на k -ом интервале [(k — 1) h; kh ], где k =1, 2, 3..., то эмпирическая интенсивность отказов на этом интервале будет равна

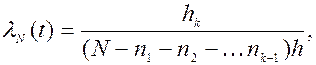(3.21)

при

(k -1) h £ t £ kh.

В формуле 3.21

N— число элементов, подвергнутых испытанию;

n_i —число элементов, отказавших на предыдущих интервалах.

Подсчитав l (t) для всех интервалов, можно по полученным значениям построить график l _N (t). Примерный вид построения функции l _N (t) приведен на рис. 3.4.

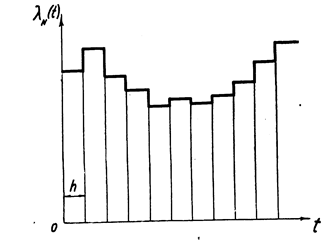
Рис. 3.4. Порядок построения функций l _N (t) по опытным данным

В общем случае кривая l(t) может иметь различный вид. Рассмотрим наиболее простой и наиболее важный частный случай кривой интенсивности отказа (рис. 3.5).

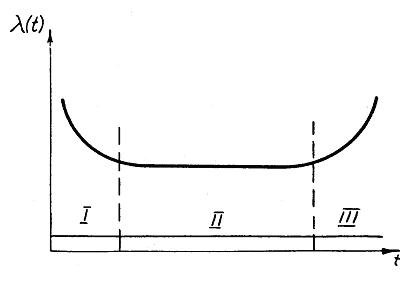
Рис. 3.5. Идеализированный вид кривой интенсивности отказов l(t).

Весь интервал по этой кривой можно разбить на 3 участка.

I — период приработки, «выжигания» дефектных элементов. В этот период выходят из строя некачественно изготовленные элементы.

II—период нормальной работы элементов.

l(t)= const или l(t)» const,

III—период форсированного «старения» в основном убыстряющегося; l(t) возрастает.

Данную кривую следует считать идеальной. Она может не получиться, если достаточно хорош контроль перед испытанием (бракуются и не испытываются элементы с дефектами). В этом случае будет отсутствовать первый участок. Кроме того, у многих элементов срок службы заканчивается раньше, чем на кривой l(t) наступит 3-й участок.

Поэтому во многих случаях можно принять, что

l(t)= l=co n s t (3.22)

Тогда функция надежности (формула 3.19) примет следующий вид:

Р (t) =еxp [-lt]. (3.23)

Формула (3.23) является выражением экспоненциального закона надежности. Для него вероятность отказа за время t равна

Q (t) =1-е^{- l t}, (3.24)

а плотность вероятности отказов

q (t) = l е^{- l t} (3.25)

Среднее время жизни для этого случая

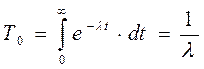(3.26)

Для экспоненциального закона интенсивность отказа обратна среднему времени. Поэтому функцию надежности можно записать и так

Р (t)=ехр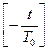 (3.27)

Часто интересующее нас время во много раз меньше среднего времени

t << T ₀ или <<1.

Тогда можно пользоваться приближенными формулами

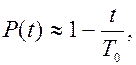(3.28)

. (3.29)

Ошибка в формулах (3.28) и (3.29) не превосходит Экспоненциальный закон очень популярен в теории надежности. Это объясняется тем, что он имеет физически естественное толкование, прост и удобен для математических расчетов.

Экспоненциальный закон обладает следующим важным свойством (по Б.В. Гнеденко).

«Вероятность безотказной работы на данном интервале (t; t +t) не зависит от времени предшествующей работы t, а зависит только от длины интервала t». Популярно выражаясь, можно сказать, если элемент в данный момент исправен, то его будущая работа (безотказность) не зависит от прошлой.

Это утверждение имеет строгое математическое доказательство, с которым можно познакомиться в работах Б.В. Гнеденко.

Однако именно за это утверждение экспоненциальный закон надежности подвергается критике. Действительно, утверждение о независимости безотказной работы элемента на участке времени t; t +t от предыдущей работы элемента, не согласуется с существующими представлениями о физике старения элементов машин и деталей. Это свойство, очевидно, следует из принятого допущения о случайной природе отказов элементов и систем.

В действительности процесс старения, по всей вероятности, следует рассматривать как два независимо действующих процесса: физически-закономерно протекающее старение и старение под воздействием случайных причин.

Поэтому экспоненциальный закон хорошо описывает надежность элементов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов, показали его недостаточную приемлемость.

Был предложен ряд других законов надежности из которых мы кратко рассмотрим два, по нашему мнению, наиважнейших.

Нормальный закон распределения, по мнению ряда исследователей, хорошо описывает процессы, протекающие с постепенными (износовыми) отказами.

При этом предполагается, что участок t_min (рис. 3.6 а), который характеризует минимальный срок жизни элемента, установленный из опыта, представляет часть времени жизни элемента с вероятностью безотказной работы Р (t)=1 (рис. 3.6 б). Поэтому характеристики надежности могут рассчитываться в интервале времени t ₁; t ₂. Вероятность безотказной работы будет равна

, (3.30)

при

t ₁ £ t £ t ₂

в формуле (3.30)

Т ₀ — среднее время жизни элемента, определяемое по формуле

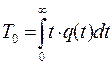(3.31)

или по формуле (3.10)

s — среднее квадратическое отклонение, равное

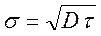(3.32)

Рис. 3.6. Графики нормального закона распределения

а) кривая плотности распределения q (t)

б) надежность - Р (t) и ненадежность - Q (t)

Для вычисления значения вероятности безотказной работы пользуются табулированной функцией Лапласа

Ф(z)=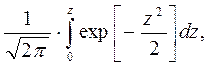 (3.33)

где z = .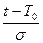

Решение формулы (3.33) представляется в виде

P (t)=0,5+Ф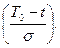 (3.34)

В формуле (3.34) применена нормированная функция Лапласа, которая изменяется в пределах

0 £ Ф(z) £0,5.

У реального элемента нередко совмещаются оба типа отказов: постепенный и внезапный. Надежность такого элемента можно определить, исходя из следующих соображений. Если P ₁(t) вероятность того, что за время t не произойдет внезапного отказа, а P ₂(t) —то же, но для постепенного отказа, то полагая:

а) что элемент работает до первого из этих отказов:

б) что отказы возникают независимо друг от друга (т. е. внезапные отказы не зависят от постепенных), — мы определим функцию надежности для такого элемента по формуле

P (t)= (3.35)

Среднее время жизни для этого случая (при s << Т ₀, а Т ₀ и 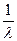одного порядка)

T 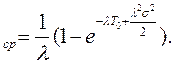(3.36)

Закон Вейбулла. Функция надежности имеет для него следующий вид

Р (t) =. (3.37)

Среднее время жизни элемента

T ₀ = (3.38)

a — дополнительный параметр.

Дисперсия времени жизни

Dt=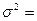 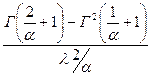(3.39)

Г- табулированная гамма-функция. Значения ее приводятся в таблицах. Интенсивность отказа

l(t)=al t (3.40)

Если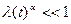, то функция Вейбулла:

Р (t)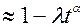 (3.41)

Вид кривых l (t) при различных значениях a приведен на рис. 3.7.

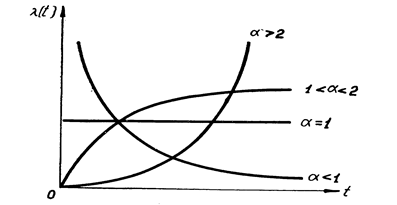
Рис. 3.7. Вид кривых l (t) при различных значениях a.

При a > 1 интенсивность отказа монотонно возрастает от 0; при a < 1 интенсивность отказа убывает монотонно и не ограничена при t = 0.

Экспоненциальный закон является частным случаем закона Вейбулла при a = 1. Закон Вейбулла получил широкое распространение, так как содержит дополнительный параметр a, подбирая который можно получить лучшее соответствие функции надежности, экспериментальным данным.

ЛИТЕРАТУРА

В.А. Наумов Основы надежности и долговечности в машиностроении. Омск: 1972. 331с.

Дата добавления: 2014-01-07