Все элементы системы имеют основное (последовательное) соединение

Надежность системы с независимыми элементами, работающими до первого отказа

Надежность технической системы

Напомним, что под технической системой понимается любое устройство, состоящее из частей, называемых элементами. Элементами могут быть как простейшие неразложимые части системы, так и отдельные узлы и агрегаты. Единственным и обязательным условием является то, что надежность всех элементов, входящих в техническую систему, должна быть известна, т. е. сосчитана заранее.

Структура системы и характер ее работы должны быть известны настолько, чтобы для любого элемента или любой группы можно сказать: вызывает ли отказ одного элемента или группы элементов отказ системы (полный или частичный).

Для вывода расчетных зависимостей, кроме указанных выше условий, введем следующее: элементы отказывают независимо друг от друга, то есть отказ любой группы элементов не изменяет надежности других элементов.

Рассмотрим вначале работу системы до ее первого отказа. В этом случае ее надежность полностью определяется функцией надежности Р (t), которая равна вероятности безотказной работы системы в течение времени t.

Пусть система состоит из п числа элементов, функцию надежности которых мы обозначим через р ₁(t); р ₂(t); …p _n(t).

Задача заключается в том, чтобы выразить функцию надежности системы Р (t) через функции надежности элементов. Рассмотрим несколько возможных случаев.

Выше указывалось, что основным или последовательным соединением считается (в, смысле надежности) такое, когда отказ одного из элементов приводит к отказу всей системы в целом. Данный случай является самым простым и самым важным.

Для безотказной работы системы в течение времени t нужно, чтобы каждый элемент работал безотказно в течение этого же времени. Так как элементы независимы в смысле надежности, то функции надежности элементов перемножаются

Р (t) =р ₁(t) × р ₂(t) ...p_n (t), (3.42)

или

P (t) =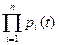. (3.43)

Выразим функции надежности через интенсивности отказов

l(t)= l₁(t) + l₂(t) +...+ l_n(t). (3.44)

При основном (последовательном) соединении элементов интенсивности отказов складываются. В частности, для экспоненциального закона, когда l _к (t)=l _к = const,

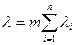(3.45)

тогда

Р (t)=exp t. (3.46)

Если надежность элементов подчиняется экспоненциальному закону, то надежность системы также будет подчиняться экспоненциальному закону.

Обозначим Т ₀ — среднее время жизни системы, а через T _к — среднее время жизни К -того элемента.

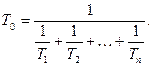(3.47)

В сложной системе всегда могут быть группы одинаковых элементов, выполняющих одинаковые функции, надежности которых можно принять одинаковыми. Для них формулы (3.42) и (3.43) запишутся так

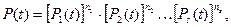(3.48)

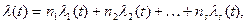(3.49)

где п_i — число элементов в группе от 1 до s.

Для экспоненциального закона

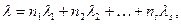(3.50)

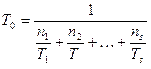(3.51)

В частном случае, когда все элементы имеют одинаковую надежность р_к (t) =р (t)

Р (t) =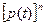 (3.52)

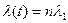(t), (3.53)

для экспоненциального закона

l=пl_i, (3.54)

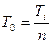. (3.55)

Определим вероятность отказа:

Q (t) = 1 -P (t) q_к (t) = 1 -P_к (t).

Тогда для основного (последовательного) соединения

Q (t) = 1 - [1 -q ₁(t)][1 -q ₂(t)] … [1 -q _n(t)]; (3.56)

Q (t)=1-

Если выполняется условие

q ₁(t) +q ₂(t) +…+q _n(t) << 1,

то можно пользоваться приближенной формулой

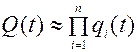(3.56)

В этом случае величина погрешности не превосходит

Дата добавления: 2014-01-07