Оценка вероятности по частоте

При испытаниях часто приходится оценивать неизвестную вероятность Р события А по его частоте 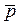в «n» независимых опытах.

В общем случае, если в «п» проведенных опытах обозначить появление события А единицей, а непоявление события — нулем, то эмпирическая вероятность будет равна

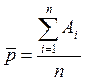
Математическое ожидание данной величины равно: М [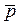] = р, а ее дисперсия: D [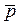] = pq/n, где q = 1 – p.

В теории вероятностей доказывается, что эта дисперсия является минимально возможной, означающей, что оценка 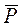является эффективной.

Доверительный интервал для вероятности 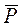будет равен I_{β( )} = (p₁; p₂),

где

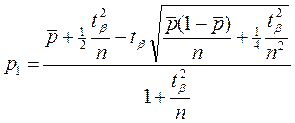
При n → ∞ величины 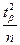→ 0 и → 0, поэтому формулы в пределе принимают вид

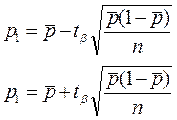
Формулами можно пользоваться при достаточно больших п (порядка сотен опытов) и когда вероятность р не слишком велика (когда величины пр и nq порядка 10 и более).

При малом числе опытом, а также в том случае, когда вероятность р очень велика или очень мала формулами для построения доверительного интервала пользоваться нельзя, т. к. они получены с рядом допущений.

В этом случае доверительный интервал строят из точного закона распределения частоты каковым является биномиальное распределение, для которого

где Р_т,п — вероятность появления т событий в п опытах, — число т сочетаний в n опытах. Частота равна .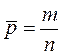

Значение доверительного интервала в этих случаях лучше не вычислять, а находить по специальным графикам. На рис. 7.2 приведен такой график для доверительной вероятности β = 0,9. В справочной литературе существуют таблицы p₁ и р₂ для различных β.

Рис. 7.2. Номограмма для определения p₁; p₂ при доверительной вероятности. β = 0.9.

Дата добавления: 2014-01-07