III. Аксиомы размерности

III₁: линейно независимая система из n векторов.

III₂: система из т+1 векторов линейно зависима.

Эта система из 12 аксиом была предложена в 1918 году известным немецким математиком Германом Вейлем (1888-1955) и называется системой аксиом Вейля.

Отметим некоторые следствия из аксиом Вейля.

Теорема 1: при любом выборе точки А вектор .

□ Пусть 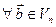, по аксиоме I такая, что 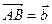. По аксиоме II для точек A,A,B имеем или. ■

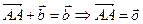Теорема 2: если 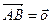, то точки A и B совпадают.

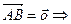□ По теореме 1 , а по условию по аксиоме I точки A и B совпадают:. ■

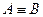Теорема 3: при любом выборе точек A и B .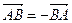

□ По аксиоме треугольника II или . ■

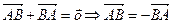Теорема 4: если , то .

□ По аксиоме треугольника II , учитывая, что по условию , получаем . По аксиоме треугольника II . ■

Теорема 5: для произвольных точек A₁, A₂,…,A_n выполняется равенство

.

!Доказать самостоятельно методом математической индукции.

Замечание 2: зафиксируем в пространстве A_n точку O. Тогда для любой точки M из А_n определен ее радиус-вектор . Из аксиомы I следует, что сопоставление точке ее радиус-вектора является биекцией. Но множество V_n бесконечно, поэтому пространство A_n содержит бесконечно много точек.

Замечание 3: очевидно, все аксиомы Вейля пространства A₃ выполняются и в элементарной геометрии, но являются там теоремами. Пространство V3 множество всех свободных векторов. Следовательно, пространство, изучаемое в школе, обладает всеми свойствами аффинного пространства, однако, оно богаче аффинного по своим свойствам. Например, в аффинном пространстве не определены важные метрические понятия элементарной геометрии: длинна отрезка, площадь фигуры, величина угла, объем тела и другие. Элементарная геометрия называется также евклидовой. Дальнейшей нашей целью является обобщение понятия евклидовой геометрии путем введения понятия многомерного евклидова пространства и аксиоматическое построения евклидовой геометрии для пространств любой конечной размерности. Первым шагом было построение аффинного пространства, обладающего лишь частью свойств евклидова пространства.

Дата добавления: 2014-01-07