
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аффинная система координат
|
|
|
|
1º. Выберем в пространстве An точку O и произвольный базис 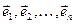 векторного пространства Vn, то есть такую упорядоченную систему векторов, что выполнены два условия:
векторного пространства Vn, то есть такую упорядоченную систему векторов, что выполнены два условия:
а) система 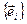 линейно независима;
линейно независима;
б) любой вектор 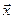 из Vn является линейной комбинацией векторов данной системы (через них линейно выражается).
из Vn является линейной комбинацией векторов данной системы (через них линейно выражается).
Известно из курса алгебры, что в пространстве Vn существуют хотя бы один базис из n векторов и любой его базис состоит также из n векторов.
Определение 1: совокупность точки O и базиса 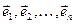 называется аффинной системой координат или аффинным репером (репер (лат.) - метка) пространства
называется аффинной системой координат или аффинным репером (репер (лат.) - метка) пространства 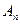 и обозначается символом
и обозначается символом  или короче
или короче 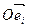 .
.
Точку O назовем началом координат, а векторы 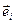 - координатными векторами. Оси проходящие через точку O в направлении векторов
- координатными векторами. Оси проходящие через точку O в направлении векторов 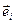 , называют координатными осями и обозначают
, называют координатными осями и обозначают 
Пусть M – произвольная точка пространства An, в котором задан репер 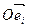 . Разложим радиус-вектор
. Разложим радиус-вектор  точки M по базису
точки M по базису 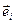 :
:
 (1)
(1)
(такое разложение всегда существует и единственно = ТЕОРЕМА)
Определение 2: числа 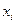 называются координатами точки M в системе координат
называются координатами точки M в системе координат 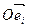 . Записывают
. Записывают 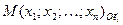 или короче
или короче  .
.
Таким образом, координатами точки M в репере 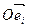 называются координаты радиус-вектора этой точки в базисе
называются координаты радиус-вектора этой точки в базисе 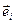 .
.
 (2)
(2)
Замечание 1: так как любой вектор имеет в данном базисе вполне определенные координаты, то координаты точки в данной системе координат определенны однозначно (установлена биекция между точками пространства An и упорядоченными наборами из n действительных чисел).
Теорема 1: координаты вектора 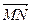 равны разностям соответствующих координат точек N и M.
равны разностям соответствующих координат точек N и M.
□ Пусть M(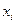 ) и N(
) и N(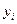 ) в репере
) в репере 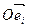 , тогда по аксиоме треугольника II
, тогда по аксиоме треугольника II  , откуда имеем
, откуда имеем  ■
■
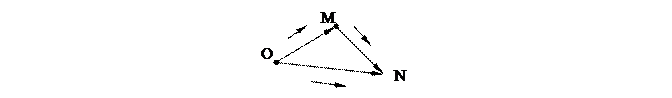
2º. Переход к новой системе координат.
Рассмотрим в пространстве An две аффинные системы координат: старую 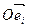 и новою
и новою 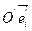
Пусть 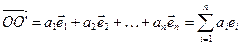 (3), то есть
(3), то есть  , а новые координатные векторы
, а новые координатные векторы  выражаются через старые
выражаются через старые 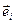 по формулам:
по формулам:
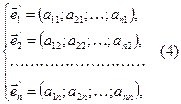
причем, так как векторы базиса линейно независимы, то 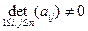 (5).
(5).
Теорема 2: если начало новой аффинной системы координат и старые и новые координатные векторы связаны соотношениями (3) и (4) при условии (5), то координаты 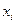 произвольной точки M в старой системе координат выражается через ее координаты
произвольной точки M в старой системе координат выражается через ее координаты  в новой системе координат по формулам.
в новой системе координат по формулам.
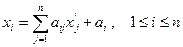 , то есть
, то есть
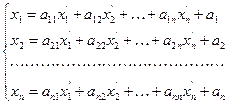 , при условии
, при условии 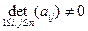 (6)
(6)
По условию имеем:


По аксиоме треугольника II имеем:
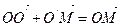 (10)
(10)
Подставим в (10) выражения из (3), (4), (8) и (7), получим следующее равенство:


Раскрыв скобки и приведя подобные слагаемые:
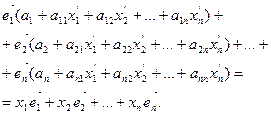 (11)
(11)
Так как координаты вектора в данном базисе определены однозначно, то коэффициенты при одинаковых векторах в левой и правой частях равенства (11) равны, следовательно, справедливы формулы (6), условие (5) также выполняется. ■
Определение 3: формулы (6) наз. формулами преобразования координат точки при переходе к новой АСК.
Замечание 2: как известно из курса алгебры, формулы преобразования координат вектора при переходе к новому базису имеют вид:
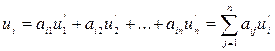 ,
, 
то есть:
 (12)
(12)
где  и
и  .
.
Упражнение: в пространстве  даны пять точек:
даны пять точек:  ,
,  ,
,  ,
, 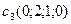 ,
,  . Записать формулы преобразования координат точек, положив:
. Записать формулы преобразования координат точек, положив:
 ,
,  ,
,  ,
,  ,
, 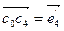 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 595; Нарушение авторских прав?; Мы поможем в написании вашей работы!