IV. Цилиндрические квадрики (цилиндры)

Рассмотрим теперь случаи, когда в уравнениях (2) и (3) из §20 m<n, а в уравнении (4) из §20 m<n-1. Положим в уравнении (2) и (3) m=r, а в уравнении (4) m=r-1. Получим следующие уравнения:

(4)

(5)

(6)

где r<n и все 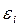равны .

Квадрики с такими уравнениями называются цилиндрическими (цилиндрами).

Замечание 4:Можно показать, что цилиндрическая квадрика состоит из параллельных друг другу (n-r) – мерных плоскостей, называемых образующими, пересекающих некоторую квадрику, называемую направляющей и лежащей в r – мерной плоскости 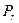. Квадрики с уравнениями (4) и (5) имеют бесконечное множество центров, являющееся (n-r)-мерной плоскостью. Так как переменная 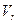содержится в уравнении в первой степени, изменение её знака приводит к другому уравнению, следовательно, (6) центров не имеет.

Примеры:

9) n=2, линии аффинной плоскости :

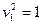- пара различных параллельных оси прямых. Образующими являются две прямые с уравнениями и 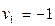, а направляющие – пара точек A(1;0) и B(-1;0), в которых эти прямые пересекают ось 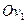с уравнением .

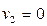- пара мнимых прямых, параллельных оси .

10) n=3, поверхности пространства .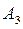

- эллиптический цилиндр.

- мнимый эллиптический цилиндр.

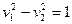- гиперболический цилиндр.

- параболический цилиндр.

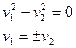- пара пересекающихся плоскостей.

- пара мнимых плоскостей, пересекающихся по действительной прямой с уравнениями .

- пара различных параллельных плоскостей.

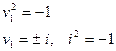- пара мнимых параллельных плоскостей.

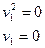- пара совпадающих плоскостей.

Остальные случаи сводятся к рассмотренным изменением нумерации координат.

Замечание 5: Сопоставление рассмотренных выше примеров показывает, что все квадрики пространства разбивается на три класса, пространства - на девять классов, пространства 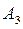- на семнадцать классов. В один класс при этом объединяются все квадрики, уравнения которых с помощью надлежащего выбора аффинной системы координат можно привести к одинаковому виду. Любые две квадрики одного класса аффинно-эквивалентны, так как формулы перехода от одной системы координат к другой и формулы аффинного преобразования пространства с алгебраической точки зрения имеют один и тот же вид.

Замечание 6: Квадрики с различными нормальными уравнениями могут оказаться одинаковыми точечными множествами. Например, мнимый эллипс и пара мнимых параллельных прямых – пустое точечное множество. Поэтому аффинно-эквивалентными могут оказаться и квадрики из различных классов. С геометрической точки зрения эти классы не различаются между собой.

Дата добавления: 2014-01-07