Симметрический оператор, его матрица, собственные значения и собственные векторы

Определение 1: Линейное отображение векторного пространства 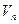в себя называется линейным оператором:

1) , 2) , .

Определение 2: Линейный оператор 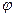евклидового векторного пространства 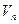называется симметрическим, если

для . (1)

То есть, символ симметрического оператора при скалярном умножении можно перенести одного вектора на другой.

если 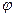- биекция

Теорема 1: симметрический линейный оператор в любом ортонормированном базисе имеет симметрическую матрицу.

□ Пусть симметрический линейный оператор 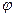имеет в ортонормированном базисе матрицу . Положим в формуле (1) и , тогда (2)

Так как векторы также являются базисными и выражаются через вектора с помощью матрицы 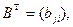то имеем:

(3) - вследствие ортогональности базиса.

Аналогично получаем

(4)

Из равенств (2), (3), (4) следует, что для любых 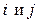, то есть матрица 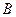- симметрическая. ■

Теорема 2(обратная): если линейный оператор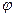 хотя бы в одном ортонормированном базисе имеет симметрическую матрицу, то он является симметрическим.

□ Пусть в ортонормированном базисе 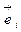матрица линейного оператора 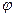симметричная: (5)

Тогда для получаем:

(6)

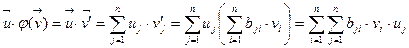и (7)

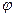Из равенств (5), (6), (7) следует, что , то есть оператор - симметрический. ■

Теорема 3: характеристическое уравнение симметрического линейного оператора 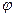может иметь только действительные корни матрицы, собственное значение вектора □■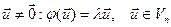

Следствие: любой симметрический линейный оператор имеет хотя бы одно собственное значение.

Замечание 2: согласно основной теореме алгебры любое алгебраическое уравнение имеет хотя бы один комплексный корень. В частности, характеристическое уравнение симметрического линейного оператора обладает этим свойством. По теореме 3 это число - действительное, оно является собственным значением данного оператора. Числа , являются решениями векторного уравнения , также действительны и представляют собой координаты собственного вектора , соответствующего собственному значению .

Теорема 4: собственные векторы симметрического линейного оператора, соответствующие его различным собственным значениям, ортогональны между собой.

□ Пусть и 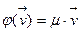причем . Так как 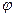- симметрический линейный оператор, то

или .

Так как , то или . ■

Теорема 5: для любого симметрического линейного оператора евклидова векторного пространства 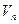существует ортонормированный базис, составленный из собственных векторов этого оператора.

□ [5], с. 99-100, Т.2 (метод математической индукции).

Следствие: матрица симметрического линейного оператора с помощью соответствующего выбора ортонормированного базиса может быть приведена к диагональному виду; этот базис состоит из нормированных собственных векторов данного оператора.

§23. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.

1º. Теорема о возможности приведения квадратичной формы к каноническому виду.

В §18 было доказано, что любая квадратичная форма может быть приведена с помощью линейного преобразования переменных к каноническому виду и нормальному видам. Это преобразование рассматривалось как переход к новому базису в векторном пространстве. В евклидовом пространстве рассматриваются лишь ортонормированные базисы, поэтому мы теперь будем пользоваться линейными преобразованиями переменных с ортогональными матрицами, то есть ортогональными преобразованиями переменных. Оказывается, что привести квадратичную форму к каноническому виду возможно с помощью только ортогональных преобразований переменных. Переход к нормальному же виду уже не всегда возможен.

Лемма: если квадратичная форма и линейный оператор имеют одну и ту же матрицу относительно какого-нибудь ортонормированного базиса, то они будут иметь одинаковые матрицы и относительно любого другого ортонормированного базиса.

□ Рассмотрим квадратичную форму:

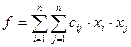(1)

и линейный оператор с одинаковыми матрицами: 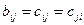. Этот оператор отображает произвольный вектор 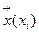на вектор 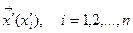по формулам

(2)

Тогда квадратичная форма (1) примет вид:

(3)

Перейдем к новому ортонормированному базису. Пусть в этом базисе

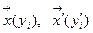, где (4)

Используя формулы (4), найдем скалярное произведение :

.

Отсюда из формулы (3) получаем:

(5)

Сравнивая равенства (4) и (5) видим, что квадратичная форма и линейный оператор имеют и в новом базисе одну и ту же матрицу с элементами . ■

Теорема: любая квадратичная форма может быть приведена к каноническому виду с помощью ортогонального преобразования переменных.

□ Пусть квадратичная форма (1) и линейный оператор имеют в ортонормированном базисе одну и ту же симметрическую матрицу, то есть 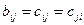. Запишем характеристическое уравнение этого оператора

(6)

По следствию из теоремы (5) §22 существует ортонормированный базис , относительно которого матрица данного линейного оператора имеет диагональный вид, где по главной диагонали стоят корни 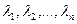характеристического уравнения (6). По лемме и квадратичная форма (1) в новом базисе будет иметь диагональную матрицу, то есть примет канонический вид:

(7)

Здесь каждый корень характеристического уравнения взят столько раз, какова его кратность.

Векторы старого и нового базисов связаны ортогональной матрицей ():

(8)

Матрица преобразования , приводящего квадратичную форму к каноническому виду, получается при транспонировании этой ортогональной матрицы, следовательно, также является ортогональной. ■

2º. Способ приведения квадратичной формы к каноническому виду:

1) Записываем и решаем характеристическое уравнение (6); его корни 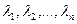являются коэффициентами при в каноническом виде (7) квадратичной формы.

2) Находим новый ортонормированный базис и формулы ортогонального преобразования, приводящего квадратичную форму к каноническому виду.

a) Пусть - однократный корень уравнения (6). Подставляем этот корень в систему линейных уравнений , при принимающую вид:

(9)

Находим из нее координаты 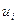собственного вектора , соответствующей этому собственного значения . Нормируя найденный вектор, получаем вектор искомого ортонормированного базиса .

b) Пусть теперь - корень характеристического уравнения кратности . После его подстановки в систему (9) найдем m линейно независимых ее решений, выбрав их так, чтобы получились координаты m попарно ортогональных единичных векторов. Примем найденные векторы за m векторов искомого базиса евклидова векторного пространства .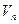

Аналогичные вычисления выполним для каждого из корней характеристического уравнения (6).Так как сумма кратностей всех корней равна 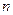, а собственные векторы соответствующие различным его корням, ортогональны, получим искомый ортонормированный базис .

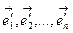3) С помощью транспонирования матрицы перехода от базиса к базису получаем матрицу ортогонального преобразования, приводящего квадратичную форму к каноническому виду. Оно имеет вид:

, (10)

где

3º. Ортогональные инварианты.

Подвергнем переменные в квадратичной форме f ортогональному преобразованию и будем рассматривать его как переход к новому ортонормированному базису евклидова векторного пространства 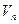. При этом преобразовании у линейного оператора, матрица которого совпадает с матрицей квадратичной формы, остаются неизменными коэффициенты характеристического многочлена. Они являются функциями элементов такой матрицы или равных им соответственно коэффициентов квадратичной формы. Так как эти выражения (функции) не меняются при ортогональном преобразовании, то они называются ортогональными инвариантами квадратичной формы.

Пример:

- характеристический многочлен линейного оператора, матрица которого совпадает с матрицей квадратичной формы.

Выражения - ортогональные инварианты квадратичной формы. Значит и корни характеристического многочлена также являются ее ортогональными инвариантами.

Дата добавления: 2014-01-07