Проективные координаты

Опр.1. Две аффинные системы координат 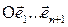и 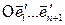в связке О (n+1)-мерного аффинного пространства A_n+1 называются эквивалентными между собой, если существует такое числ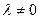о , что

...,

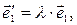
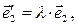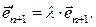
Относительно двух эквивалентных координатных систем любой луч m связки О, а значит и любам точка М проективного пространства RPⁿ, имеет одни и те же наборы координат.

Опр. 2. Класс эквивалентных между собой аффинных координатных систем в связке О пространства A_n+1 называется системой проективных координат в связке О.

Опр. 3. Наборами координат любого луча m и любой гиперплоскости а в связке О относительно данной системы проективных координат называются наборы координат этого луча и этой гиперплоскости относительно любой аффинной системы координат в связке О. Переименовав связку О в проективное пространство RPⁿ, получаем, что каждая проективная координатная система в проективном пространстве RPⁿ задается n+2 точками, из которых никакие n+1 не лежат в одной гиперплоскости: (n+1)-ой вершиной Е₁, Е₂,..., Е_n+1 координатного многогранника и единичной точкой Е. Эти n+2 точек называются фундаментальными точками данной координатной системы.

В арифметическом n-мерном проективном пространстве имеется «привилегированная» или «однородная» система координат, определенная точками Е₁(1;0;...;0), Е₂(0;1;...;0),..., Е_n+1(0;0;...;1), Е(1;1;...;1). В этой «однородной» системе координат наборами координат любой точки из RPⁿ служат те числовые наборы, классом которых и является данная точка M(х₁,х₂,..., х_n+1).

Наряду с «однородной» системой координат в пространстве RPⁿ может быть задана и другая «новая» система координат {E'₁ Е'₂,..., E'_n+1}, Е наборами координат своих фундаментальных точек:

E'_k(c_1k; c_2k;...; c_n+1,k), где 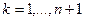, E'(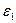,,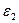…,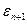). (1)

Всегда можно сделать так, что эти n+2 наборы (1) окажутся согласованными между собой в смысле векторного равенства:

,

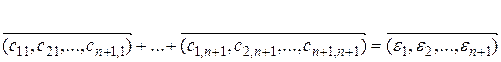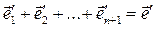, где .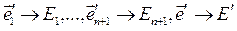

При этом однородные координаты x₁, х₂,..., х_n+1 произвольной точки М связаны с проективными координатами 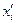этой же точки в системе координат {E'₁ Е'₂,..., E'_n+1} формулами преобразования координат вида:

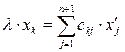, (2)

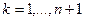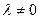, - произвольный числовой множитель, det(c_kj)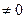

Замечание. Из формул (2) следует, что переход от исходной «однородной» системы координат к новой системе проективных координат в n-мерном проективном пространстве RPⁿ осуществляется с помощью невырожденной квадратной матрицы порядка n+1, причём всегда возможен и обратный переход.

Дата добавления: 2014-01-07