Проективно-аффинное пространство

Опр.1. Проективное пространство, в котором какая-нибудь одна гиперплоскость выделена из остальных и названа «несобственной» или «бесконечно удаленной», называется проективно-аффинным пространством.

Рассмотрим, каким образом можно выделить в n-мерном проективном пространстве RPⁿ его «несобственные» элементы точки, прямые, двумерные плоскости и т.д.

Пусть в n+1-мерном аффинном пространстве А_n+1 дано n-мерное подпространство А_n и в нём - аффинная система координат . Назовём аффинную систему координат 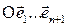пространства А_n+1 естественно связанной с координатной системой n-мерного пространства А_n, если начало О системы координат 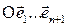не лежит в пространстве А_n. Первые n координатных векторов у этих координатных систем общие: 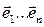, а последний вектор 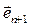есть вектор 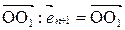. Тогда в системе координат подпространство А_n пространства А_n+1 задаётся уравнением: . Возьмём теперь в пространстве A_n+1 связку с центром О. Если произвольная точка М гиперплоскости А_n имеет в системе координаты 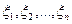, то координаты этой точки М в системе 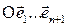следующие: 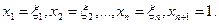Поэтому наборами координат луча 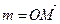связки О являются все наборы х₁,х₂,...,х_n+1, пропорциональные набору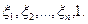

Опр. 2. Все такие указанные наборы называются наборами однородных координат точки М в системе однородных координат, соответствующей аффинной координатной системе .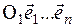

Итак, однородные координаты х₁,х₂,...,х_n+1 точки М связаны с её аффинными координатами 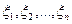в системе пропорцией: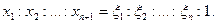

Отсюда аффинные координаты выражаются через однородные по формулам: .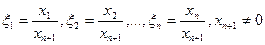

Опр. 3. Соответствие между точками М гиперплоскости А_n и лучами 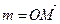связки О называется перспективным соответствием.

При этом каждой точке М гиперплоскости А_n, имеющей однородные координаты х₁,х₂,...,х_n+1 соответствует луч связки О с такими же координатами в системе .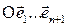

Обратно, каждому лучу m(х₁,х₂,...,х_n+1) связки О, у которого последняя координата 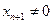, соответствует точка М гиперплоскости А_n с теми же координатами х₁,х₂,...,х_n+1. Однако, лучам m связки О, у которых 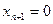, не соответствует никакая точка М гиперплоскости А _n. Чтобы сделать перспективное соответствие между связкой О и гиперплоскостью А_n взаимно однозначным или биективным, дополним эту гиперплоскость несобственными или бесконечно удалёнными точками с наборами однородных координат х₁,х₂,...,х_n,0. Пополненная таким образом гиперплоскость превращается в проективное пространство RPⁿ = 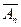. Это пространство становится арифметическим, если отождествить каждую его точку М с классом наборов ее однородных координат.

Замечание. Арифметическое проективное пространство естественно рассматривать как проективное пространство, полученное от пополнения несобственными элементами обыкновенного n-мерного аффинного пространства А_n с заданной в нём системой аффинных координат . Несобственные точки этого пространства - это точки (х₁,х₂,...,х_n+1), для которых 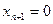, причем все такие точки принадлежат несобственной гиперплоскости с уравнением: 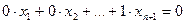или 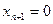. Преимущество однородной системы координат состоит в том, что несобственные точки получают вполне определенные координаты.

Дата добавления: 2014-01-07