При этом согласно закону инерции квадратичных форм, число положительных коэффициентов, т. е. индекс квадратичной формы, в любом нормальном виде её одно и то же

Для формы ранга k индекс может принимать значения k,k-1,…,1,0. при умножении квадратичной формы на (-1) форма ранга k и индекса r переходит в форму ранга k и индекса k-r. Поэтому квадрика, заданная в однородных координатах уравнением (1), где квадратичная форма имеет ранг k, может быть задана в новой проективной системе координат уравнением вида:

(3)

где у переменных опущены штрихи, все , а число положительных среди них равно k,k-1,…,.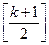

Замечание 2. Формулы указанного выше линейного преобразования переменных можно понимать и как формулы перехода от одной координатной системы к другой, и как формулы некоторого проективного преобразования пространства RPⁿ=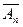. Кроме того, без ограничения общности можно считать, что в уравнении (3) квадрики ранга k члены с положительными коэффициентами предшествуют членам с отрицательными коэффициентами.

Имеем основной результат:

Всякая квадрика ранга k может быть с помощью проективного преобразования пространства RPⁿ=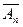переведена в квадрику, уравнение которой в исходной однородной системе координат пространства RPⁿ имеет один из следующих видов:

(4)

Всего имеется ровно 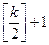таких уравнений.

Общее число нормальных видов квадрик в пространстве RPⁿ выражается формулой: (5)

При этом, если n чётно, т. е. n=2 l, то S= l ²+3 l +1;

если n нечётно, т. е. n=2 l -1, то S= l ²+2, где .

В частности, на проективной плоскости RP² при n=2 и l =1 имеется пять различных нормальных форм. В трёхмерном проективном пространстве RP³ при n=3 и l =2 имеется восемь различных нормальных форм.

Опр 2. Две квадрики проективного пространства RPⁿ называются проективно-эквивалентными, если с помощью проективного преобразования этого пространства одна из них может быть переведена в другую.

Замечание 3. Выше установлено, что каждая квадрика пространства RPⁿ попадает в один из S(n) классов, каждый из которых определен уравнением вида (4). При этом все квадрики из одного класса проективно эквивалентны. Можно доказать, что две квадрики из различных классов проективно не эквивалентны между собой (проективно различны). Поэтому полученные S(n) классов дают полную проективную классификацию действительных квадрик n-мерного действительного проективного пространства.

Дата добавления: 2014-01-07