
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
|
|
|
|
Схема независимых испытаний Бернулли. Полиноминальное распределение
Предположим, что производятся независимо друг от друга n испытаний, в каждом из которых возможны только 2 исхода: успех и неудача («У»,»Н»). Причём вероятность успеха Р(У)= p, Р(Н)= q, p+q =1.
Определение 10.1. Последовательность 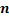 испытаний называется испытаниями Бернулли, если эти испытания независимы, в каждом из них возможны 2 исхода, причём вероятности этих исходов не меняются от испытания к испытанию.
испытаний называется испытаниями Бернулли, если эти испытания независимы, в каждом из них возможны 2 исхода, причём вероятности этих исходов не меняются от испытания к испытанию.
В n испытаниях Бернулли элементарным исходом является:
(ω1, ω2,…, ω n), где ω i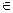 {У,Н}, i
{У,Н}, i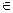 {1,…, n }.
{1,…, n }.
Всего таких исходов 2 n. Поскольку испытания независимы, то:
Р(ω1, ω2,…, ω n)= Р(ω1)P(ω2)…P(ω n).
Обозначим через Pn(k) вероятность того, что в n испытаниях Бернулли произошло ровно k успехов. Тогда
P n (k)=Р{(У,…,У,Н,…,Н),(У,…,У,Н,У,Н,…,Н),…,(Н,…,Н,У,…У)}=
= pkqn-k + pkqn-k + …+ pkqn-k = 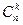 pkqn-k.
pkqn-k.
Таким образом получим
P n (k)= 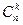 pkqn-k, k
pkqn-k, k 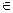 {0,…, n }, p+q =1 – формула Бернулли.
{0,…, n }, p+q =1 – формула Бернулли.
Пример 10.2. Двое равных по силам шахматистов играют в шахматы. Что вероятнее: выиграть одну партию из двух или две из четырёх? Ничьи во внимание не принимаются.
 p=q=
p=q=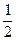 , P2(1)=
, P2(1)= 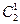 ∙
∙ 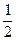 ∙
∙ 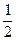 =
=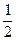 =
= ;
;
P4(2)= 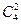 ∙ (
∙ (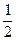 )2 ∙ (
)2 ∙ (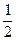 )2=6∙
)2=6∙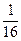 =
=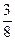 ;
;
Таким образом P2(1)> P4(2).
Полиноминальное распределение
Предположим, что производится независимо друг от друга n испытаний, в каждом из которых возможны k исходов E1, E2,…, E k. Вероятность этих исходов обозначим P(E i)= pi, i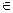 {1,…, k }. Причём
{1,…, k }. Причём 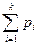 =1, k >2.Вероятность того, что в n испытаниях исход E1 появится r1 раз, E2
=1, k >2.Вероятность того, что в n испытаниях исход E1 появится r1 раз, E2 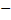 r2 раз, …, E1 – rk раз, где
r2 раз, …, E1 – rk раз, где 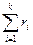 = n, находится по формуле:
= n, находится по формуле:
P(r1, r2,…, rk)=

 …
… ,
, 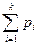 =1,
=1, 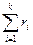 = n – формула полиноминального распределения.
= n – формула полиноминального распределения.
Замечание 10.3. Формула полиноминального распределения обобщает формулу Бернулли на случай более 2 исходов в каждом испытании.
Пример 10.4. В урне 3 шара: белый, красный, синий. Из урны 5 раз наудачу извлекаются шары с возвращением. Найти вероятность того, что белый шар извлечён 3 раза, а красный и синий –по одному разу.
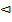 Поскольку p1 = p2 = p3=
Поскольку p1 = p2 = p3= 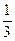 ; r1 =3, r2 =1, r3 =1.
; r1 =3, r2 =1, r3 =1.
Тогда P5(3, 1,1)= ∙ (
∙ (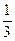 )3 ∙
)3 ∙ 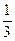 ∙
∙ 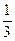 = 20∙
= 20∙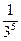 =
= 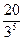 =
=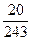 .
. 
Теорема 11.1. (Пуассона) Пусть производится n независимых испытаний, в каждом из которых событие А наступает с вероятностью р. Тогда, если число испытаний неограниченно возрастает, а p →0, причём n∙p=a – величина постоянная, то P n (k)
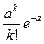 .
.
 По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях
По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях
P n (k)= 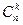 pkqn-k=
pkqn-k=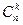 pk (1 - p) n-k.
pk (1 - p) n-k.
Отсюда
P n (k)= 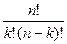 pk (1 - p) n-k=
pk (1 - p) n-k= pk (1 - p) n-k.
pk (1 - p) n-k.
По условию a=n∙p p=
p=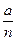 , подставляя, получим:
, подставляя, получим:
P n (k)= 

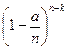 =
=
=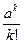
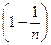
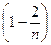 …
…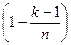
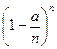
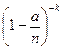 =
=
=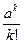
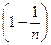
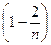 …
…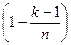
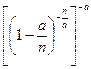
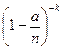 .
.
Переходя к пределу при n →∞
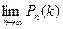 =
= 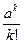
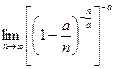
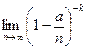 =
= 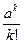
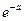 [ т.к.
[ т.к. 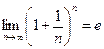 ].
]. 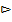
Замечание 11.2. Теоремой Пуассона удобно пользоваться, когда p →0, причём a=n∙p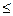 10. Существуют специальные таблицы, в которых приведены значения вероятностей для различных параметров a и k.
10. Существуют специальные таблицы, в которых приведены значения вероятностей для различных параметров a и k.
Формула Бернулли удобна, когда значение n не очень велико. В противном случае используют приближенные формулы из теорем Муавра-Лапласа.
Теорема 11.3. (локальная теорема Муавра-Лапласа) Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0< p <1, то вероятность того, что событие A появится ровно k раз в n независимых испытаниях
P n (k)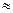
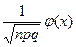 , где
, где 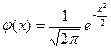 – малая функция Лапласа,
– малая функция Лапласа,  , q =1- p.
, q =1- p.
Имеются специальные таблицы значений функции  . Нужно учитывать, что функция
. Нужно учитывать, что функция  – чётная, т.е.
– чётная, т.е. 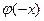 =
= .
.
Теорема 11.4. (интегральная теорема Муавра-Лапласа) Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от отлична от 0 и 1, т.е. 0< p <1, то вероятность того, что событие А появится от k1 до k2 раз в n независимых испытаниях, определятся выражением:
P n (k1,k2)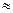
 , где
, где 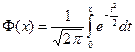 – функция Лапласа,
– функция Лапласа, 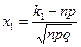 ,
, 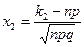 , q =1- p.
, q =1- p.
Функция Лапласа – нечётная, т.е.  . Значения находят по таблице.
. Значения находят по таблице.
Пример 11.5. Пусть вероятность события А в каждом отдельном испытании p =0,8. Найти вероятность того, что событие А появится 75 раз в 100 независимых испытаниях.
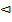 По локальной теореме Муавра-Лапласа х =
По локальной теореме Муавра-Лапласа х =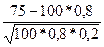 =
=  = –1,25. Значение
= –1,25. Значение 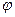 (–1,25)=
(–1,25)=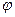 (1,25)=0,1826 находится по таблице.
(1,25)=0,1826 находится по таблице.
Тогда вероятность
P100(75)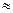
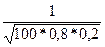 *0,1826
*0,1826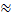 0,04565.
0,04565.
Пример 11.6. Вероятность Р(А) появления события А в одном испытании равна 0,8. Найти вероятность того, что событие А появится более 69 раз в 100 независимых испытаниях.
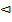 n =100, p =0,8, q =0,2, k1= 70, k1= 100.
n =100, p =0,8, q =0,2, k1= 70, k1= 100.
По интегральной теореме Муавра-Лапласа 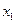 =
=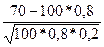 =
=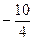 = –1,25,
= –1,25, 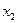 =
= =
= = 5. По таблице
= 5. По таблице  (-2,5)= -
(-2,5)= - (2,5)= -0,4938,
(2,5)= -0,4938,  (5)=0,5, P100(70,100)
(5)=0,5, P100(70,100)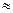
 (5) -
(5) - (-2,5)=0,5+0,4938=0,9938
(-2,5)=0,5+0,4938=0,9938
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2370; Нарушение авторских прав?; Мы поможем в написании вашей работы!