Интерференция поляризованных лучей. Эллиптическая и круговая поляризация

Лучи, обыкновенный и необыкновенный, возникающие при двойном лучепреломлении из естественного свети, не когерентны. Если естественный луч разложить па два луча, поляризованных в двух различных плоскостях А и В, а затем с помощью поляризационного прибора привести колебания в них к одной плоскости, то они не интерферируют. Это объясняется тем, что в естественном свете колебания, происходящие в разных плоскостях, испущены различными атомами или молекулами, следовательно, друг с другом не связаны и не имеют постоянных разностей фаз (не когерентны)

Лучи же, обыкновенный и необыкновенный, возникающие из одного и того же поляризованного луча, когерентны. Если колебания в двух таких лучах привести с помощью поляризационного прибора к одной плоскости, то лучи будут интерферировать обычным образом. Если колебания в двух когерентных плоско поляризованных лучах происходят во взаимно перпендикулярных направлениях, то они складываются как два взаимно перпендикулярных колебательных движения и приводят к возникновению колебаний эллиптического характера.

Световые волны, электрический вектор в которых меняется со временем так, что его конец описывает эллипс, называются эллиптически поляризованными. В частном случае эллипс может превратиться к круг и тогда мы имеем дело со светом, поляризованным по кругу. Магнитный вектор в волне всегда перпендикулярен к электрическому и в волнах рассматриваемого типа также меняется со временем таким образом, что его конец описывает эллипс или круг.

Рассмотрим случай возникновения эллиптических волн подробнее. В § 4 мы видели, что при нормальном падении пучка лучей на пластинку из одноосного кристалла, оптическая ось в которой параллельна преломляющей поверхности, обыкновенный и необыкновенный лучи идут по одному направлению, но с разными скоростями. Пусть на такую пластинку падает плоско поляризованный луч, плоскость поляризации которого составляет с плоскостью главного сечения пластинки угол, отличный от 0 и от π/2. Тогда в пластинке возникнут оба луча, обыкновенный и необыкновенный, и они будут когерентны. В момент их возникновения в пластинке разность фаз между ними равна нулю, но она будет возрастать по мере проникновения лучей в пластинку. Подсчитаем эту разность фаз.

Каждый из лучей при прохождении сквозь пластинку толщиной l отстанет по фазе на величину 2π l/λ, где λ — длина волны данного луча в кристалле. Для обыкновенного луча длина волны λ₀ = υ₀/ν, где υ₀ — скорость его распространения в кристалле, а ν — частота колебаний. Так как υ₀= c/n ₀, где п ₀—коэффициент преломления обыкновенного луча, то . Так же получим для длины волны необыкновенного луча в кристалле выражение 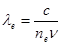, где п_е - коэффициент преломления необыкновенного луча. Отсюда разность фаз между обоими лучами равна:

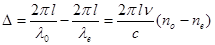
Так как с /ν — длина волны в пустоте λ, то:

Таким образом, разность фаз между обоими лучами тем больше, чем больше разность между коэффициентами преломления п _o — п _e и чем больше толщина кристалла l. Если толщину пластинки подобрать так, чтобы Δ= k π, где π — целое число, то оба луча, выйдя из пластинки, снова дадут плоско поляризованный луч. При k четном его плоскость поляризации совпадает с плоскостью поляризации луча, падающего на пластинку; при k нечетном плоскость поляризации вышедшего из пластинки луча окажется повернутой на π /2 по отношению к плоскости поляризации луча, падающего на пластинку. При всех иных значениях разности фаз Δ колебания обоих лучей, вышедших из пластинки, складываясь, дадут эллиптическое колебание. Если Δ=(2 k+ 1) π /2, то оси эллипса совпадут с направлениями колебаний в обыкновенном и необыкновенном лучах (рис. 6.1).

Амплитуды колебаний в обыкновенном и необыкновенном лучах определятся углом, который составляет плоскость поляризации падающего на пластинку луча с плоскостью главного сечения пластинки. Амплитуды обоих лучей будут равны друг другу, если плоскость поляризации падающего луча составит угол в 45° с плоскостью главного сечения пластинки. В этом случае эллипс превратится и круг и, следовательно, возникнет свет, поляризованный по кругу.

Наименьшая толщина пластинки, способной превратить плоско поляризованный луч в луч, поляризованный по кругу (Δ = π /2), определится равенством,

откуда получаем:

Такая пластинка даст разность хода между обыкновенным и необыкновенным лучами, равную λ/4, поэтому она сокращенно называется пластинкой в четверть волны. Очевидно, что пластинка в четверть волны даст разность хода между обоими лучами, равную λ/4, лишь для света данной длины волны λ. Для света других длин волн она даст разность хода, несколько отличную от λ/4, как из-за прямой зависимости l от λ, так и из-за зависимости от λ разности коэффициентов преломления п _o — п _e.

Очевидно, наряду с пластинкой в четверть длины волны, можно изготовить и пластинку „ в полдлины волны ", т. е. такую пластинку, которая вносит между обыкновенным и необыкновенным

лучами разность хода λ/2, чему соответствует разность фаз π. По сказанному, такая пластинка может употребляться для поворачивания плоскости поляризации плоско поляризованного света на π/2.

Как указано, с помощью пластинки λ/4 из плоско поляризованного луча можно получить луч, поляризованный эллиптически или по кругу; обратно, из эллиптически поляризованного или поляризованного по кругу луча с помощью пластинки λ/4 можно получить свет, плоско поляризованный.

Этим обстоятельством пользуются, чтобы отличить свет, поляризованный эллиптически, от частично поляризованного, или свет, поляризованный по кругу, от естественного. Одного только поляризационного прибора, например николя, недостаточно, чтобы различить эти типы поляризации лучей. Действительно, в случае как эллиптически поляризованного света, так и частично поляризованного при поворачивании николя наблюдается лишь изменение яркости света между некоторыми максимальным и минимальным значениями. В случае света, поляризованного по кругу, или естественного, при любом поворачивании николя яркость света останется неизменной. Если же предварительно ввести пластинку λ/4, соответственным образом ее ориентировав, то эллиптически поляризованный свет превратится в прямолинейно поляризованный и сможет быть потушен николем. Частично же поляризованный свет не претерпит изменений при прохождении через пластинку λ/4. Также свет, поляризованный по кругу, можно отличить от естественного на основании того обстоятельства, что пропущенный через пластинку λ/4 он будет тушиться николем.

Указанный анализ эллиптически поляризованного света можно произвести с помощью пластинки λ/4 в том случае, когда эллиптическая поляризация возникает в результате сложения двух взаимно перпендикулярных колебаний разной амплитуды с разностью фаз π/2. Если же эллиптическая поляризация возникает в результате сложения двух взаимно перпендикулярных колебаний с разностью фаз Δ ≠ π/2, то для превращения такого света в плоско поляризованный надо ввести такую добавочную разность фаз Δ', которая в сумме с Δ дала бы разность фаз, равную π (или 2k π). В этих случаях вместо пластинки λ/4 употребляются особые приборы, носящие название компенсаторов, которые позволяют получить любое значение разности фаз Δ.

Дата добавления: 2014-01-07