Уравнения Максвелла. Электромагнитное поле

Лекция 2.12.

Ток смещения.

Теория электромагнитного поля, начала которой заложил Фарадей, математически была завершена Максвеллом. При этом одной из новых важнейших идей, вы­двинутых Максвеллом, была мысль о симметрии во взаимоза­висимости электрического и магнитного полей. А именно, по­скольку меняющееся во времени магнитное поле (dΒ/dt) созда­ет электрическое поле (см. (2.11.6)), следует ожидать, что меняющееся во времени электрическое поле (dΕ/dt) создает магнитное поле.

К этой идее о необходимости существования по сути нового явления индукции можно прийти путем, например, следую­щих рассуждений. Мы знаем, что согласно теореме о цирку­ляции вектора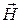

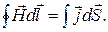(2.12.1)

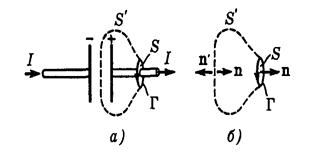Применим эту теорему к случаю, когда предварительно заря­женный плоский конденсатор разряжается через некоторое внешнее сопротивление (рис. a). В качестве контура Г, по которому определяем циркуляцию 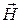, возьмем кривую, охватывающую провод. На контур Г можно натянуть разные поверхности, например S и S’. Обе поверхно­сти имеют «равные права», однако через поверхность S течет ток I, а через поверхность S’ не течет никакого тока. Получается, что циркуляция вектора 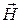зависит от того, какую поверхность мы натягиваем на данный контур, чего явно не может быть (в случае постоянных токов этого и не проис­ходило).

А нельзя ли как-то изменить правую часть (2.12.1), чтобы избе­жать этой неприятности? Оказывается, можно, и вот как.

Первое, что мы замечаем, это то, что поверхность S’ «прони­зывает» только электрическое поле. По теореме Гаусса поток вектора 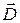сквозь замкнутую поверхность 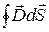= q, откуда

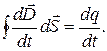(2.12.2)

С другой стороны, согласно уравнению непрерывности

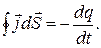(2.12.3)

Сложив по отдельности левые и правые части уравнений (2.12.2) и (2.12.3), получим

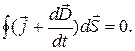(2.12.4)

Это уравнение аналогично уравнению непрерывности для по­стоянного тока. Из него видно, что кроме плотности тока про­водимости имеется еще одно слагаемое 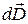/dt, размерность которого равна размерности плотности тока. Максвелл назвал это слагаемое плотностью тока смещения:

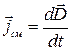. (2.12.5)

Сумму же тока проводимости и тока смещения называют пол­нымтоком. Его плотность

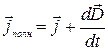. (2.12.6)

Согласно (2.12.4) линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения.

Сейчас мы убедимся в том, что введение полного тока устра­няет трудность, связанную с зависимостью циркуляции векто­ра 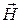от выбора поверхности, натягиваемой на контур Г. Ока­зывается, для этого достаточно в правой части уравнения (2.12.1) вместо тока проводимости ввести полный ток, т. е. ве­личину

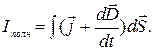(2.12.7)

В самом деле, правая часть (2.12.7) представляет собой сумму тока проводимости I и тока смещения I_см: I_полн = I + I_см. По­кажем, что полный ток I_полн будет одинаков и для поверхности S, и для поверхности S’, натянутых на один и тот же контур Г. Для этого применим (2.12.4) к замкнутой поверхности, со­ставленной из поверхностей S и S’ (рис. б). Учитывая, что для замкнутой поверхности нормаль n направлена наружу, запишем

I_полн(S’)+I_полн(S)=0.

Теперь, если обернуть нормаль n ’ для поверхности S ’ в ту же сторону, что и для S, то первое слагаемое в последнем уравне­нии изменит знак, и мы получим

I_полн(S’) =I_полн(S),

что и требовалось доказать. Итак, теорему о циркуляции век­тора 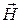, которая была установлена для постоянных токов, можно обобщить для произвольного случая и записать

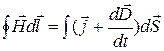. (2.12.8)

В таком виде теорема о циркуляции вектора 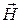справедлива всегда, свидетельством чему является согласие этого уравне­ния с результатами опыта во всех без исключения случаях.

Несколько замечаний о токе смещения. Следует иметь в виду, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Токи смещения существуют лишь там, где меняется со време­нем электрическое поле. Даже в вакууме всякое изменение во времени электрического поля возбуждает в окружающем пространстве магнитное поле.

В диэлектриках ток смещения состо­ит из двух существенно различных слагаемых. Так как вектор 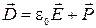, то отсюда видно, что плотность тока смещения 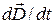складывается из «истинного» тока смещения 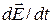и тока поляризации 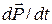— величины, обусловленной движе­нием связанных зарядов. В том, что токи поляризации возбу­ждают магнитное поле, нет ничего неожиданного, ибо эти то­ки по природе своей не отличаются от токов проводимости, так как связаны с движением зарядов. Принципиально новое содержится в утверждении, что и дру­гая часть тока смещения 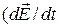), которая не связана ни с каким движением зарядов, а обусловлена только изменением электрического поля, также возбуждает магнитное поле.

Открытие этого явления — наиболее существенный и решаю­щий шаг, сделанный Максвеллом при построении теории электромагнитного поля. Это открытие вполне аналогично от­крытию электромагнитной индукции, согласно которому пе­ременное магнитное поле возбуждает вихревое электрическое поле. Следует также отметить, что открытие Максвеллом тока смещения — чисто теоретическое открытие, причем первосте­пенной важности.

Уравнения Максвелла в интегральной форме.

С введением тока смещения макроскопическая теория электромагнитного поля была блестяще завершена. Открытие тока смещения 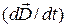позволило Максвеллу создать единую теорию электри­ческих и магнитных явлений. Теория Максвелла не только объяснила все разрозненные явления электричества и магне­тизма (причем с единой точки зрения), но и предсказала ряд новых явлений, существование которых подтвердилось впо­следствии.

До сих пор мы рассматривали отдельные части этой теории. Теперь можно представить всю картину в виде системы фун­даментальных уравнений электродинамики, называемых урав­нениями Максвелла внеподвижных средах. Этих уравнений четыре (мы уже познакомились с каждым из них в отдельно­сти в предшествующих разделах, а сейчас просто соберем их все вместе). В интегральной форме система уравнений Мак­свелла имеет следующий вид:

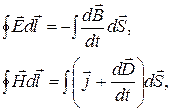
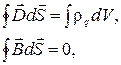(2.12.9)

где ρ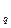— объемная плотность сторонних зарядов, — плотность тока проводимости.

Эти уравнения в сжатой форме выражают всю совокупность наших сведений об электромагнитном поле.

Содержание этих уравнений заключается в следующем:

1. Циркуляция вектора по любому замкнутому контуру рав­на со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным кон­туром. При этом под понимается не только вихревое элек­трическое поле, но и электростатическое (циркуляция послед­него, как известно, равна нулю).

2. Поток вектора 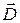сквозь любую замкнутую поверхность ра­вен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.

3. Циркуляция вектора 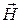по любому замкнутому контуру рав­на полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.

4. Поток вектора сквозь произвольную замкнутую поверх­ность всегда равен нулю.

Из уравнений Максвелла для циркуляции векторов и 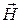сле­дует, что электрическое и магнитное поля нельзя рассматри­вать как независимые: изменение во времени одного из этих полей приводит к появлению другого. Поэтому имеет смысл лишь совокупность этих полей, описывающая единое электро­магнитное поле.

Если же поля стационарны (= const и = const), то уравне­ния Максвелла распадаются на две группы независимых урав­нений:

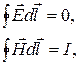
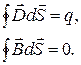(2.12.10)

В этом случае электрическое и магнитное поля независимы друг от друга, что и позволило нам изучить сначала постоян­ное электрическое поле, а затем независимо от него и посто­янное магнитное поле.

Необходимо подчеркнуть, что рассуждения, с помощью кото­рых можно придти к уравнениям Максвелла, ни в коей мере не могут претендовать наих доказательство. Эти уравнения нель­зя «вывести», они являются основными аксиомами, постула­тами электродинамики, полученными путем обобщения опыт­ных фактов. Эти постулаты играют в электродинамике такую же роль, как законы Ньютона в классической механике или начала термодинамики.

Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют по­верхности разрыва — поверхности, на которых свойства сре­ды или полей меняются скачкообразно.В этих уравнениях содержатся и граничные условия, которые име­ют уже знакомый нам вид:

D_1n=D_2n, E_1τ=E_2τ, B_1n=B_2n, H_1τ=H_2τ (2.12.11)

(здесь первое и последнее условия относятся к случаям, когда на границе раздела нет ни сторонних зарядов, ни токов прово­димости). Заметим также, что приведенные граничные усло­вия справедливы как для постоянных, так и для переменных полей.

Материальные уравнения. Фундаментальные уравнения Мак­свелла еще не составляют полной системы уравнений электро­магнитного поля. Этих уравнений недостаточно для нахожде­ния полей по заданным распределениям зарядов и токов.

Уравнения Максвелла необходимо дополнить соотношениями, в которые входили бы величины, характеризующие индивиду­альные свойства среды. Эти соотношения называют матери­альными уравнениями. Вообще говоря, эти уравнения доста­точно сложны и не обладают той общностью и фундаменталь­ностью, которые свойственны уравнениям Максвелла.

Материальные уравнения наиболее просты в случае достаточно слабых электромагнитных полей, сравнительно медленно ме­няющихся в пространстве и во времени. В этом случае для изотропных сред, не содержащих сегнетоэлектриков и ферро­магнетиков, материальные уравнения имеют следующий вид (он нам уже знаком):

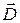=εε₀, =μμ₀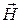, =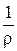(+*), (2.12.12)

где ε, μ, 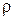— известные нам постоянные, характеризующие электрические и магнитные свойства среды (диэлектрическая и магнитная проницаемости и удельное сопротивление). * — на­пряженность поля сторонних сил, обусловленная хи­мическими или тепловыми процессами.

Свойства уравнений Максвелла

Уравнения Максвелла линейны. Они содержат только первые производные полей и по времени и пространственным координатам и первые степени плотности электрических зарядов и токов. Свойство линейности уравнений Максвелла непосредственно связано с принципом суперпозиции: если два каких-нибудь поля удовлетворяют уравнениям Максвелла, то это относится и к сумме этих полей.

Уравнения Максвелла выполняются во всех инерциальных системах отсчета. Они являются релятивистски-инвариантными. Это есть следствие принципа относительности, согласно которому все инерциальные системы отсчета физически эквивалентны друг другу. Факт инвариантности уравнений Максвелла (относительно преобразований Лоренца) подтверждается многочисленными опытными данными. Вид уравнений Максвелла при переходе от одной инерциальной системы отсчета к другой не меняется, однако входящие в них величины преобразуются по определенным правилам.

О симметрии уравнений Максвелла. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено опять же тем, что в природе существуют электрические заряды, но нет зарядов магнитных (насколько известно в настоящее время). Вместе с тем в нейтральной однородной непроводящей среде, где плотность зарядов и плотность тока проводимости равны нулю, уравнения Максвелла приобретают симметричный вид:

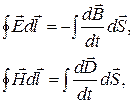
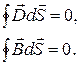(2.12.13)

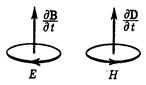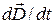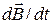Симметрия уравнений относительно электрического и магнитного полей не распространяется лишь на знак перед производными d/dt и . Различие в знаках перед этими производными показывает, что линии вихревого электрического поля, индуцированного изменением поля , образуют с вектором левовинтовую систему, в то время как линии магнитного поля, индуцируемого изменением 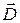, образуют с вектором 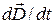правовинтовую систему (см. рисунок).

Электромагнитные волны. Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Поля такого рода называют электромагнитными волнами. В вакууме они всегда распространяются со скоростью, равной скорости света c.

Выяснилось также, что ток смещения (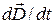) играет в этом явлении первостепенную роль. Именно его присутствие наряду с величиной 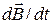и означает возможность появления электромагнитных волн. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля электрического, в свою очередь, возбуждает магнитное поле. За счет непрерывного взаимопревращения или взаимодействия они и должны сохраняться ‑ электромагнитное возмущение будет распространяться в пространстве.

Теория Максвелла не только предсказала возможность существования электромагнитных волн, но и позволила установить все их основные свойства.

Энергия электромагнитного поля.

Если среда не содержит сегнетоэлектриков и ферромагнетиков (т.е. нет явления гистерезиса) и отсутствуют токи проводимости, то плотность энергии электромагнитного поля (в соответствии с (2.6.10) и (2.11.19)) будет определяться по формуле

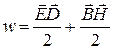. (2.12.14)

Дата добавления: 2014-01-07