
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определители 3-го и n-го порядков
|
|
|
|
Рассмотрим систему трех линейных уравнений с тремя неизвестными.
 11Х1 +
11Х1 + 12Х2 +
12Х2 +  13Х3 = b1
13Х3 = b1
 21Х1 +
21Х1 + 22Х2 +
22Х2 +  23Х3 = b2 (1)
23Х3 = b2 (1)
 31Х1 +
31Х1 + 32Х2 +
32Х2 +  33Х3 = b3
33Х3 = b3
Матрицу этой системы обозначим А
А=
Исключим Х2 и Х3 из системы (1). Для этого первое уравнение умножим на
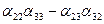 ,
,
второе уравнение умножим на
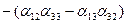 ,
,
третье уравнение умножим на
 ,
,
и результаты умножения сложим.
Прежде, чем выполнять указанные выше умножения и сложения, полезно отметить, что множители сконструированы по одному и тому же правилу. Чтобы убедиться в этом, запишем их, используя определители 2-го порядка.
 . (2)
. (2)
Отметим, что определитель второго порядка в правой части равенства (2) соответствует квадратной матрице второго порядка, полученной из матрицы А вычеркиванием строки и столбца, содержащих элемент  , а показателем степени числа (-1) является сумма индексов этого элемента.
, а показателем степени числа (-1) является сумма индексов этого элемента.
 . (3)
. (3)
Определитель второго порядка в правой части равенства (3) соответствует квадратной матрице второго порядка, полученной из матрицы А вычеркиванием строки и столбца, содержащих элемент  , а показателем степени числа (-1) является сумма индексов этого элемента.
, а показателем степени числа (-1) является сумма индексов этого элемента.
 . (4)
. (4)
Определитель второго порядка в правой части равенства (4) соответствует квадратной матрице второго порядка, полученной из матрицы А вычеркиванием строки и столбца, содержащих элемент  , а показателем степени числа (-1) является сумма индексов этого элемента.
, а показателем степени числа (-1) является сумма индексов этого элемента.
Важно отметить, что вычеркиваемые элементы  ,
, и
и  являются элементами первого столбца.
являются элементами первого столбца.
Проделав элементарные, но громоздкие преобразования (упомянутые выше умножения и сложения), после исключения Х2 и Х3 из системы (1).получим
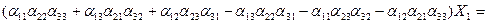
= (5)
(5)
Число
 =
= 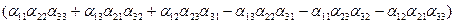 (6)
(6)
назовем определителем матрицы А или определителем третьего порядка.
Ниже будет дано детальное словесное описание формулы (6).
Здесь же отметим, что, решая систему двух уравнений, мы получили выражение, аналогичное (5),
(
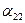 -
-
 )Х1 = (
)Х1 = (
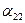 -
-
 )
)
и назвали число  = (
= (
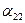 -
-
 ) определителем второго порядка.
) определителем второго порядка.
Обозначения определителя матрицы А третьего порядка такие же, как и для определителя 2-го порядка:
 = detA =
= detA =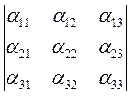 (7)
(7)
При вычислении определителя третьего порядка удобно пользовать известным правилом Сарруса.
Легко заметить, что число в правой части равенства (5), которое обозначим  1, можно получить, если в выражении (6)
1, можно получить, если в выражении (6)  заменить на b1,
заменить на b1,  заменить на b2,
заменить на b2,  заменить на b3. Это означает, что
заменить на b3. Это означает, что  1 является определителем матрицы А1. которая получается из матрицы А заменой первого столбца столбцом правых частей системы (1).
1 является определителем матрицы А1. которая получается из матрицы А заменой первого столбца столбцом правых частей системы (1).
А1=
 1 =
1 = =
= .
.
Введенные выше обозначения позволяют записать соотношение (5) в виде
 X1=
X1= 1 , (8)
1 , (8)
либо в виде
 X1 =
X1 = (9)
(9)
 1 – определитель в правой части равенства (9) является определителем матрицы А1. которая получается из матрицы А заменой первого столбца столбцом правых частей системы (1).
1 – определитель в правой части равенства (9) является определителем матрицы А1. которая получается из матрицы А заменой первого столбца столбцом правых частей системы (1).
Аналогично, исключая Х1 и Х3 из системы (1) и используя при этом вместо (2), (3) и (4) другие множители (можно догадаться какие, если вспомнить правило их конструирования), придем к соотношениям
 X2=
X2= 2 , (10)
2 , (10)
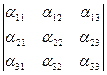 X2 =
X2 =  (11)
(11)
 2 – определитель в правой части равенства (11) является определителем матрицы А2. которая получается из матрицы А заменой второго столбца столбцом правых частей системы (1).
2 – определитель в правой части равенства (11) является определителем матрицы А2. которая получается из матрицы А заменой второго столбца столбцом правых частей системы (1).
А2 = 
Аналогично, используя вместо (2), (3) и (4) другие множители (можно догадаться какие) придем к соотношениям
 X3=
X3= 3 , (12)
3 , (12)
 X3 =
X3 =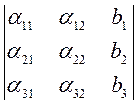 (13)
(13)
 3 – определитель в правой части равенства (13) является определителем матрицы А3. которая получается из матрицы А заменой третьего столбца столбцом правых частей системы (1).
3 – определитель в правой части равенства (13) является определителем матрицы А3. которая получается из матрицы А заменой третьего столбца столбцом правых частей системы (1).
А3 = 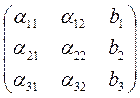
Если  ≠ 0, тогда система (1) имеет единственное решение, которое находится по формулам Крамера.
≠ 0, тогда система (1) имеет единственное решение, которое находится по формулам Крамера.
X1= 1 /
1 / ,
,
X2= 2 /
2 / , (14)
, (14)
X3= 3 /
3 / .
.
В самом деле, если предположить, что существует другое решение, то оно при  ≠ 0 тоже будет определяться формулами Крамера, т. е. решение единственно.
≠ 0 тоже будет определяться формулами Крамера, т. е. решение единственно.
Случай 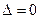 рассмотрим позже. Сейчас же нашей целью является не выяснение вопроса о решениях системы (1), а вскрытие математической природы определителя n-го порядка, изучение его свойств, отправляясь от определителя 3-го порядка,
рассмотрим позже. Сейчас же нашей целью является не выяснение вопроса о решениях системы (1), а вскрытие математической природы определителя n-го порядка, изучение его свойств, отправляясь от определителя 3-го порядка,
Итак, прежде чем сформулировать определение определителя 3-го, а заодно и определителя n-го порядка изучим формулу (6).
 =
= 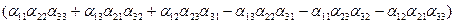
Отметим, что каждое слагаемое в ней представляет собой произведение трех элементов, принадлежащих разным строкам и столбцам матрицы А. Всего слагаемых 3! = 6, а первые индексы элементов каждого слагаемого одинаковы и расположены в порядке возрастания, Перед слагаемым ставится плюс, если количество нарушений порядка среди вторых индексов четное или ноль. Знак минус ставится, если количество нарушений порядка среди вторых индексов нечетно. Например, во втором слагаемом для вторых индексов 3, 1, 2 отмечается два нарушения порядка: 3 стоит перед 1, и 3 стоит перед 2. В последнем слагаемом для вторых индексов 2, 1, 3 наблюдается только одно нарушение порядка.
Сформулируем теперь определение определителя третьего порядка. Ценность этого определения состоит в том, что оно дословно повторяет определение определителя порядка n.
Определение 1. Определителем квадратной матрицы 3-го (n-го) порядка называется число, которое вычисляется по 32 (по n2) элементам матрицы и представляет собой алгебраическую сумму 3! (n!) всех возможных произведений из 3-х (из n) элементов матрицы, взятых по одному из каждой строки и каждого столбца. Знак каждого слагаемого определяется по числу (-1)N, где N – число нарушений порядка среди вторых индексов, при условии, что в каждом из произведений первые индексы элементов матрицы следуют в порядке возрастания.
Итак, формулы для определителей второго и третьего порядка достаточно подробно разъяснены (они выведены), отмечены закономерности построения определителя третьего порядка. Эти закономерности распространяются и на определителя порядка. n.
После изучения свойств определителя мы покажем, как выводятся формулы Крамера для системы линейных уравнений с квадратной матрицей произвольного порядка n.
Второе определение определителя
Перебор всех вариантов выбора элементов по одному из каждой строки и каждого столбца оказывается слишком громоздким даже для определителя четвертого порядка (даже в этом простом случае число слагаемых оказывается большим, равным 4!=24) и поэтому определение 1 на практике не используется. Определением 1 можно пользоваться лишь при вычислении определителей третьего порядка, что тоже не желательно.
Покажем другой способ вычисления определителя 3-го порядка (сведение задачи к вычислению трех определителей второго порядка). Этот способ оказывается пригодным и для определителей порядка n (задача сводится к вычислению n определителей (n-1)–го порядка).
В формуле (6) сгруппируем члены, содержащие элементы первой строки, получим
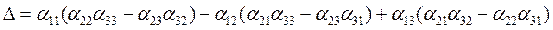 (15)
(15)
Иначе эта формула перепишется так:
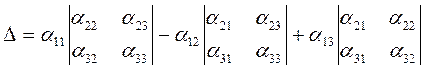 (16)
(16)
В формуле (16) можно перед всеми слагаемыми поставить знак плюс, если переписать ее в виде.
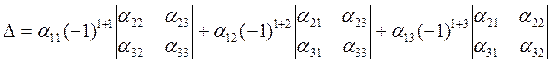 (17)
(17)
Формула (17) – это иначе переписанная формула (15) или формула (16). Легко убедиться, что знак минус в (17) выбирается автоматически с помощью (-1) в степени (i+j), где i – номер строки элемента, стоящего перед определителем в формулах (16) и (17), а j – номер столбца этого элемента.
Отметим, что формула (17) - это разложение определителя третьего порядка по элементам первой строки.
Важность введения множителя (-1)(i+j) заключается в том, что этот множитель позволяет автоматически выбирать знак перед каждым слагаемым не только в разложении определителя третьего порядка, но и в разложении определителя произвольного порядка n.
Используя специальные обозначения для определителей второго порядка, запишем (17) в виде
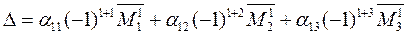 . (18)
. (18)
Здесь определитель 
 называется минором элемента
называется минором элемента  ,
, 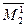
 называется минорам элемента
называется минорам элемента  ,
, 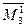
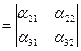 называется минором элемента
называется минором элемента 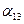 . Легко проверить, что миноры
. Легко проверить, что миноры  ,
, 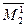 ,
, 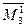 получаются из определителя
получаются из определителя 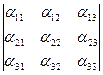 вычеркиванием строки и столбца, в которых расположены соответственно элементы
вычеркиванием строки и столбца, в которых расположены соответственно элементы  ,
,  ,
, 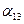 (черта над М означает вычеркивание).
(черта над М означает вычеркивание).
Отметим, что часто элементы матрицы А называют также элементами определителя этой матрицы, что упрощает математические формулировки, хотя определитель – это просто число, а у числа нет никаких элементов.
Используя знак суммы, запишем формулу (18) в виде
 (19)
(19)
Используя формулу (19), можно сформулировать другое определение определителя третьего порядка. Но особая ценность полученной формулы (19) заключается в том, что она легко обобщается на случай определителя порядка n, а именно: чтобы получить выражение, аналогичное (19), для определителя произвольного порядка, вместо цифры 3 над знаком суммы в (19) нужно поставить n.
 . (20)
. (20)
В формуле (20)  - элементы первой строки матрицы порядка n
- элементы первой строки матрицы порядка n




 A
A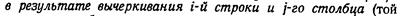

Определение 2 Определителем квадратной матрицы n-го порядка называется число
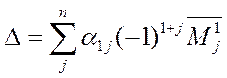 , (20)
, (20)
которое обозначается

Здесь  - миноры элементов
- миноры элементов  первой строки
первой строки

Если положить n=3, то получим формулу (19)..
Определение 2 указывает способ вычисления определителя. Вычисление определителя порядка n сводится к вычислению n миноров элементов первой строки, т. е. к вычислению n определителей (n-1)–го порядка. Таким образом, многократное применение формулы (20) позволяет свести вычисление определителя порядка n к вычислению определителей 2-го порядка.
Формула (20) – это разложение определителя по элементам первой строки.
Разложение определителя по элементам любой строки и любого столбца.
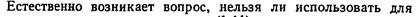
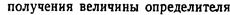
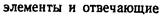
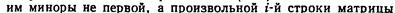 .
.
Теорема 1. 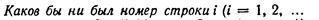
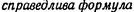
Оказывается определитель можно разлагать и по элементам любого столбца.
Теорема 2 


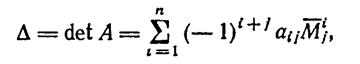
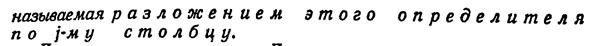
Теоремы 1 и 2 доказываются методом математической индукции.
Ниже приведен пример разложения определителя четвертого порядка по элементам третьего столбца.
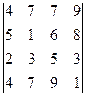 =7(-1)1+3
=7(-1)1+3  +6(-1)2+3
+6(-1)2+3  +5(-1)3+3
+5(-1)3+3  +9(-1)4+3
+9(-1)4+3 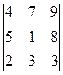
Свойства определителей

Транспонированную матрицу обозначают также символом АТ.



Это свойство докажем методом математической индукции, но сначала кратко об этом методе.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!