
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод математической индукции
|
|
|
|
Индукция – это метод рассуждений, ведущий от частных примеров к общему выводу.
В математике для доказательства утверждений относительно натурального числа n (утверждение далее будем обозначать А(n)) часто применяется метод математической индукции.
Приведем примеры утверждений A(n):
1) Число 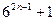 делится на 7 при любом натуральном n.
делится на 7 при любом натуральном n.
2) При любом n число P = n2 + n + 41 является простым числом. (Неверное утверждение)
3) Если h > -1 и h ≠ 0, то 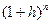 >
> при любом натуральном n
при любом натуральном n 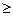 2. (неравенство Бернулли).
2. (неравенство Бернулли).
4) Перестановка двух строк не изменяет абсолютной величины определителя порядка n, а знак меняет на противоположный..
Для того чтобы убедиться в справедливости утверждения A(n), нужно доказать, что оно верно при любом натуральном n, т. е. нужно проверить это утверждение при
n=1
n=2
n=3
.
.
.
Очевидно, что бесконечное число проверок при всех натуральных n выполнить невозможно.
Оказывается, что этого и не надо делать, если выполнить только одну проверку при n=1, а затем предположить. что утверждение A(n) верно при n = к и, используя это предположение, доказать A(n) верно при n = к+1.
В самом деле, пусть проверено утверждение
(A(n) верно при n=1). (*)
Пусть, кроме того, доказано, что из предположения о верности A(n) при n = к следует, что A(n) верно при n = к+1, т. е. доказано.
(A(n) верно при n=к)  (A(n) верно при n=к+1) (**)
(A(n) верно при n=к+1) (**)
1) При n=1 согласно (**) имеем
(A(n) верно при n=1)  (A(n) верно при n=2). (1)
(A(n) верно при n=2). (1)
Здесь (A(n) верно при n=1) уже не предположение, а доказанное (проверенное) утверждение (см (*)).
2) При n=2 согласно (**) имеем
(A(n) верно при n=2)  (A(n) верно при n=3). (2)
(A(n) верно при n=3). (2)
3) При n=3 согласно (**) имеем
(A(n) верно при n=3)  (A(n) верно при n=4). (3)
(A(n) верно при n=4). (3)
4) При n=4 согласно (**) имеем
(A(n) верно при n=4)  (A(n) верно при n=5). (4)
(A(n) верно при n=5). (4)
.и т. д.
Таким образом, убеждаемся, что утверждение A(n) справедливо при любом n, и при этом ничего доказывать не надо, раз доказано (**).
Схема метода математической индукции
1) Проверить, что утверждения A(n) верно при n=1.
2). Предположить, что A(n) верно при n=к.
3). Используя предположение (A(n) верно при n=к). доказать, что
A(n) верно при n = к+1.
Теперь приступим к доказательству свойства 2о.
Докажем свойство 2о для определителя порядка n

1). Поскольку самая маленькая матрица, в которой можно переставить строки, - это матрица второго порядка, то проверим свойство 2о при n=2.
 =
=
 = -
= - 
2). Предположим, что свойство 2о верно для всякого определителя порядка k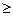 2
2
3). Докажем, что свойство 2о верно при n = k+1.
Для этого запишем определитель порядка k+1 в виде разложения по одной из строк, которая не переставляется. Не нарушая общности, разложим его по первой строке.

Поменяем местами две строки. Это могут быть любые две строки, кроме первой. Сразу отметим, что при перестановке выбранных строк, переставляются также две строки в определителях  . Определитель с переставленными строками обозначим
. Определитель с переставленными строками обозначим 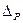 . Запишем разложение
. Запишем разложение 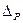 по первой строке.
по первой строке.

Здесь миноры элементов первой строки обозначены буквой  . Они отличаются от определителей
. Они отличаются от определителей  , тем, что в них две строки переставлены. Но по предположению индукции для определителей
, тем, что в них две строки переставлены. Но по предположению индукции для определителей  и
и  порядка k имеем
порядка k имеем  = -
= -  , т. е.
, т. е.
 ,
,
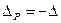 .
.
Таким образом, согласно принципу математической индукции свойство 2о справедливо для определителя любого порядка n
Далее нам потребуется операция умножения матрицы на число.
При умножении матрицы на число все элементы матрицы умножаются на это число.
Если матрица состоит из одного столбца, то при умножении на число все элементы столбца умножаются на это число.

Линейное свойство сформулируем для столбцов, но оно, конечно, справедливо и для строк
Если в определителе
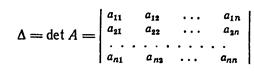
некоторый столбец 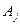 с номером j является линейной комбинацией двух столбцов C и S с коэффициентами
с номером j является линейной комбинацией двух столбцов C и S с коэффициентами 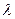 и
и 
 ,
, 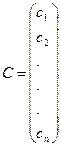 ,
, 
 =
=
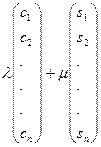 ,
,
то 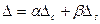 , где
, где 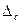 - определитель, у которого j-й столбец равен С, а все остальные столбцы те же, что и у
- определитель, у которого j-й столбец равен С, а все остальные столбцы те же, что и у  , а
, а  - определитель, у которого j-й столбец равен S, а все остальные столбцы те же, что и у
- определитель, у которого j-й столбец равен S, а все остальные столбцы те же, что и у  ,
,
Пример. 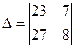
 =
= 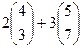
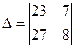 =
= +
+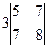
Для доказательства свойства 3о каждый из определителей  ,
, 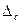 и
и  разложим по элементам j-го столбца и заметим, что у всех трех определителей миноры j-го столбца
разложим по элементам j-го столбца и заметим, что у всех трех определителей миноры j-го столбца 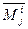 одинаковы. Формула
одинаковы. Формула 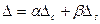 сразу вытекает из равенства
сразу вытекает из равенства
 =
=
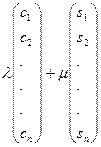 ,
,
которое переписывается в виде
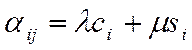 .
.


Три основных свойства и пять следствий, вытекающих из этих свойств, следует применять при вычислении определителей.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 758; Нарушение авторских прав?; Мы поможем в написании вашей работы!