
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула полной вероятности
|
|
|
|
Расчет работоспособности цепей
1. оба прибора соединены последовательно






 Сигнал
Сигнал
Р1 Р2
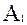 работает первый
работает первый
 работает второй
работает второй
А сигнал прошел по цепи
А =  ∙
∙
 и
и  независимы
независимы
Р(А) = Р( )∙Р(
)∙Р( )=
)=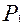
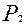
2. приборы подключены параллельно









 Р1
Р1
Р2
 ∙
∙ совместные события
совместные события
а) А =  +
+
Р(А) = Р( )+Р(
)+Р( ) - Р(
) - Р( ∙
∙ ) =
) =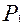 +
+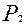 -
-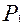
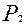
б) А = 
 +
+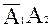 +
+  ∙
∙
в) Ā = 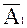 ∙
∙
Р(Ā) = Р(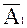 ) ∙ Р(
) ∙ Р( )= (1-
)= (1-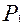 )∙(1-
)∙(1-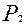 )
)
Р(А) = 1- (1-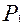 )∙(1-
)∙(1-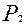 )
)
Предположим, что в результате некоторого опыта происходит одно из попарно не совместных событий  Вместе с тем в рамках этого опыта рассматривается событие А
Вместе с тем в рамках этого опыта рассматривается событие А

А=  +
+ + … +
+ … +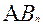
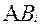
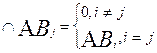
Р(А)= 
Р(А) 
Замечание:

|
Пример: На сборочный ковер поступают однотипные детали с 3-х заводов равными партиями. В продукции 1-го завода брак – 5%, 2-го завода – 7%, 3-го завода – 1%. Какова вероятность, что случайно взятая с конвейера деталь бракованная?
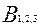 случайно выбранная деталь изготовленная 1,2,3 заводом (несовместные события)
случайно выбранная деталь изготовленная 1,2,3 заводом (несовместные события)
А – случайно выбранная деталь бракованная
Р(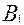 ) = Р(
) = Р( )=Р(
)=Р( )=
)= 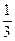
Какова вероятность того что брак взят с 1,2 или 3 завода
P(A|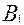 ) = 0.05
) = 0.05
P(A|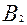 ) = 0.07
) = 0.07
P(A| ) = 0.01
) = 0.01
Р(А) = 
Задача о разорении игрока.
Подбрасывается монетка. Перед броском игрок предугадывает результат. Если угадал + 1 рубль, не угадал – 1 рубль. Начальный капитал Х рублей. Игра продолжается до тех пор пока он не наберет а (а>x) рублей или разорится. Какова вероятность, что игрок разорится.
Р(х) - вероятность разорения при начальном капитале в х рублей
Р(х+1) - вероятность разорения при угаданном первом броске
Р(х-1) – вероятность разорения при не угаданном первом броске
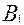 - игрок угадывает 1-е выпадение монеты
- игрок угадывает 1-е выпадение монеты
 - игрок не угадывает 1-е выпадение монеты
- игрок не угадывает 1-е выпадение монеты
А – игрок разорился
Р(А) 
Р(х)=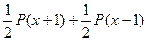
 приращение постоянно
приращение постоянно
Р(х) – линейная функция
Р(х)=
Р(0)=1 Р(0)=1=
Р(а)=0 Р(а)=0= +
+ 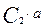
Р(х)= 1-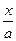
Формула вероятностей гипотез. (Формула Байеса)
Пусть в результате опыта происходит одно из несовместных событий  . Известно, также что в ходе этого опыта произошло событие А
. Известно, также что в ходе этого опыта произошло событие А
Какова вероятность, что событие А произошло в рамках события 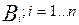
До проведения опыта вероятности  определялись следующими значениями
определялись следующими значениями 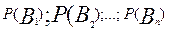 это априорные(доопытные) вероятности. После того как событие А произошло необходимо пересмотреть вероятности событий
это априорные(доопытные) вероятности. После того как событие А произошло необходимо пересмотреть вероятности событий  как условные
как условные  это апостериорное (послеопытные) вероятности
это апостериорное (послеопытные) вероятности 
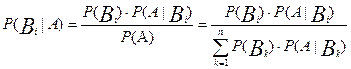 Формула Байеса
Формула Байеса
Пример: Имеется два внешне одинаковых ящика с шарами
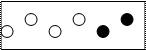 |  |
Из произвольного взятого ящика случайным образом выбирают шар. Он оказался белым. Какова вероятность что это ящик номер № 1
А – достали белый шар

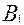 -достали белый шар из 1-го ящика события
-достали белый шар из 1-го ящика события
не совместны
 - достали белый шар из 2-го ящика
- достали белый шар из 2-го ящика
Р(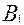 ) = Р(
) = Р( )=
)=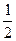 P(A|
P(A|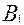 ) =
) = 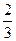 P(A|
P(A|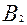 ) =
) = 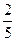
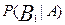 =
=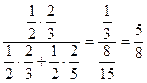
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 318; Нарушение авторских прав?; Мы поможем в написании вашей работы!