Аппроксимация функций методом наименьших квадратов

Постановка задачи аппроксимации по МНК. Условия наилучшего приближения.

Если набор экспериментальных данных получен со значительной погрешностью, то интерполяция не только не требуется, но и нежелательна! Здесь требуется построить кривую, которая воспроизводила бы график исходной экспериментальной закономерности, т.е. была бы максимально близка к экспериментальным точкам, но в то же время была бы нечувствительна к случайным отклонениям измеряемой величины.

Введем непрерывную функцию φ (x) для аппроксимации дискретной зависимости f (x _i), i = 0… n. Будем считать, что φ (x) построена по условию наилучшего квадратичного приближения, если

. (1)

Весу ρ для i -й точки придают смысл точности измерения данного значения: чем больше ρ, тем ближе аппроксимирующая кривая «притягивается» к данной точке. В дальнейшем будем по умолчанию полагать ρ = 1 для всех точек.

Рассмотрим случай линейной аппроксимации:

φ (x) = c ₀ φ ₀(x) + c ₁ φ ₁(x) + … + c _m φ _m(x), (2)

где φ ₀… φ _m ­– произвольные базисные функции, c ₀… c _m – неизвестные коэффициенты, m < n. Если число коэффициентов аппроксимации взять равным числу узлов, то среднеквадратичная аппроксимация совпадет с интерполяцией Лагранжа, при этом, если не учитывать вычислительную погрешность, Q = 0.

Если известна экспериментальная (исходная) погрешность данных ξ, то выбор числа коэффициентов, то есть величины m, определяется условием:

. (3)

Иными словами, если , число коэффициентов аппроксимации недостаточно для правильного воспроизведения графика экспериментальной зависимости. Если 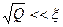, многие коэффициенты в (2) не будут иметь физического смысла.

Для решения задачи линейной аппроксимации в общем случае следует найти условия минимума суммы квадратов отклонений для (2). Задачу на поиск минимума можно свести к задаче поиска корня системы уравнений , k = 0… m. (4).

Подстановка (2) в (1), а затем расчет (4) приведет в итоге к следующей системе линейных алгебраических уравнений:

Далее следует решить полученную СЛАУ относительно коэффициентов c ₀… c _m. Для решения СЛАУ обычно составляется расширенная матрица коэффициентов, которую называют матрицей Грама, элементами которой являются скалярные произведения базисных функций и столбец свободных коэффициентов:

,

где , , j = 0… m, k = 0… m.

После того как с помощью, например, метода Гаусса найдены коэффициенты c ₀… c _m, можно построить аппроксимирующую кривую или вычислить координаты заданной точки. Таким образом, задача аппроксимации решена.

Аппроксимация каноническим полиномом.

Выберем базисные функции в виде последовательности степеней аргумента x:

φ ₀(x) = x ⁰ = 1; φ ₁(x) = x ¹ = x; φ _m(x) = x ^m, m < n.

Расширенная матрица Грама для степенного базиса будет выглядеть следующим образом:

.

Особенность вычислений такой матрицы (для уменьшения количества выполняемых действий) состоит в том, что необходимо сосчитать только элементы первой строки и двух последних столбцов: остальные элементы заполняются сдвигом предшествующей строки (за исключением двух последних столбцов) на одну позицию влево. В некоторых языках программирования, где отсутствует быстрая процедура возведения в степень, пригодится алгоритм расчета матрицы Грама, представленный далее.

Выбор базисных функций в виде степеней x не является оптимальным с точки зрения достижения наименьшей погрешности. Это является следствием неортогональности выбранных базисных функций. Свойство ортогональности заключается в том, что для каждого типа полинома существует отрезок [ x ₀, x _n], на котором обращаются в нуль скалярные произведения полиномов разного порядка:

, j ≠ k, ρ ­– некоторая весовая функция.

Если бы базисные функции были ортогональны, то все недиагональные элементы матрицы Грама были бы близки к нулю, что увеличило бы точность вычислений, в противном случае при 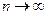определитель матрицы Грама очень быстро стремится к нулю, т.е. система становится плохо обусловленной.

Блок-схема алгоритма формирования матрицы Грама и аппроксимации полиномом.

Аппроксимация ортогональными классическими полиномами.

Представленные ниже полиномы, относящиеся ко многочленам Якоби, обладают свойством ортогональности в изложенном выше смысле. То есть, для достижения высокой точности вычислений рекомендуется выбирать базисные функции для аппроксимации в виде этих полиномов.

1) Полиномы Чебышева.

Определены и ортогональны на [–1, 1] с весом . В интервал ортогональности всегда можно вписать область определения исходной функции с помощью линейных преобразований.

Строятся следующим образом (рекуррентная формула):

T ₀(x) = 1;

T ₁(x) = x;

T _k+1(x) = 2 xT _k(x) – T _k–1(x).

2) Полиномы Лежандра.

Определены и ортогональны на [–1, 1] с весом .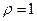

Строятся следующим образом (рекуррентная формула):

L ₀(x) = 1;

L ₁(x) = x;

.

Сглаживание и линейная регрессия.

Рассмотрим несколько наиболее простых с точки зрения программной реализации случаев аппроксимации (сглаживания).

1) Линейная регрессия.

В случае линейного варианта МНК (линейная регрессия) φ (x) = a + bx можно сразу получить значения коэффициентов a и b по следующим формулам:

,

,

где , .

2) Линейное сглаживание по трём точкам.

3) Линейное сглаживание по пяти точкам.

Дата добавления: 2014-01-07