Электронные преобразователи и аппараты. Цель лекции:рассмотреть вопросы: методы расчета и моделирование электромагнитных процессов в силовых цепях преобразователей

Лекция 9.

Цель лекции: рассмотреть вопросы: методы расчета и моделирование электромагнитных процессов в силовых цепях преобразователей.

МЕТОДЫ РАСЧЕТА И МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ПРОЦЕССОВ В СИЛОВЫХ ЦЕПЯХ ПРЕОБРАЗОВАТЕЛЕЙ

Аналитические, численные и численно-аналитические методы расче­та. Силовые схемы электронных преобразователей представляют собой электрические цепи с переменной структурой, изменяющейся в процессе функционирования вследствие циклического переключения СПП и изменения контуров с токами. В преобразователях с перемен­ной структурой наиболее часто используют аналитические, численные и численно-аналитические методы расчета процессов.

В аналитических методах силовые цепи преобразователей с пере­менной структурой и известными моментами переключения (комму­тации) СПП описываются линейными дифференциальными уравне­ниями, порядок и значения коэффициентов которых могут изменяться в моменты коммутации.

Общим методом расчета процессов в таких преобразователях яв­ляется метод разностных уравнений. Он предполагает двухэтапное составление единых уравнений для переходного и установившегося режимов: на первом этапе находят уравнения процессов без определе­ния начальных условий для отдельных интервалов периода работы, а на втором — формируют систему разностных уравнений, из решения которой определяют единые уравнения процессов. В этом методе в наиболее завершенном виде используется алгоритм, основанный на использовании теории графов и матриц для составления и решения разностных уравнений.

Если моменты переключения СПП заранее неизвестны (например, для выпрямителей), то найти при определенных допущениях аналити­ческое решение задачи расчета можно обобщенным методом анализа процессов в преобразователях [14].

Аналитические методы сопряжены с выполнением трудоемких матричных преобразований, большим объемом вычислений при на­хождении корней характеристических полиномов. Поэтому при ис­пользовании ЭВМ чаще используют численные методы.

Численные методы расчета электромагнитных процессов в сило­вых цепях преобразователей ориентированы на применение ЭВМ, поэтому их представляют в виде последовательности ряда закончен­ных этапов. Одним из основных этапов является формирование урав­нений схемы преобразователя и их решение.

Применение математических моделей СПП позволяет выполнить формирование системы уравнений схемы 1 раз, а затем только изме­нять коэффициенты этой системы при коммутациях, что требует не­больших вычислительных затрат. Затруднение вызывают сильно от­личающиеся по своему значению сопротивления СПП в открытом и закрытом состояниях, что приводит к большому разбросу постоян­ных времени (жесткости) системы дифференциальных уравнений, поэ­тому требуются значительные вычислительные ресурсы. Выходом из затруднения при расчете является использование 5-модели СПП, "об­ходящей" проблему жесткости системы дифференциальных уравне­ний. При замене СПП 5-моделью (идеальный ключ) формирование системы уравнений происходит после каждой коммутации. Это сокра­щает требуемый вычислительный ресурс. Формирование системы уравнений определяется выбором независимых переменных. Выбор в качестве независимых переменных токов обусловливает формирова­ние методов контурных токов. Если независимыми принимаются потенциалы, то используют метод узловых потенциалов. Однако оба метода не дают хороших результатов. Поэтому при формировании системы уравнений более применим метод переменных состояния, обеспечивающий получение уравнений в гибридном координатном базисе. При описании используют дифференциальные уравнения и связанные с ними алгебраические уравнения. Для контроля состояний СПП в процессе расчета необходимо определять токи открытых и напряжения закрытых СПП, что приводит к расширению базиса пере­менных. В этом случае систему уравнений формируют в полном ко­ординатном базисе, содержащем токи и напряжения всех элементов цепи, а затем ее разделяют на систему дифференциальных уравнений относительно токов и систему алгебраических уравнений относитель­но напряжений.

Для решения уравнений применяют численные методы интегриро­вания дифференциальных уравнений (чаще всего метод Рунге—Кутта) и методы решения алгебраических уравнений.

Преимуществом аналитических методов является возможность по­лучения результата без расчета предшествующего переходного про­цесса. Достоинством численных методов является простота исследо­вания схем высокого порядка. Но расчет можно завершить только после вычисления предшествующего переходного процесса. Так как основной объем вычислений в численных методах приходится на рас­чет всех периодов переходного процесса, а в аналитических — на решение систем уравнений состояния одного периода, то, очевидно, целесообразно совместить указанные методы таким образом, чтобы трудоемкость расчета установившихся процессов уменьшилась. Со­вмещение элементов аналитических и численных методов лежит в основе численно-аналитических методов расчета процессов в преоб­разователях.

Модели компонентов силовых цепей преобразователей. Одной из основных задач расчета и проектирования преобразователей является адекватное описание процессов в силовых цепях при использовании кусочно-линейных моделей элементов. Широко используют линейные модели сопротивлений, дросселей, конденсаторов. Для учета частот­ных свойств дросселей и конденсаторов применяют соответствующие эквивалентные RLC-схемы. Если же элементы нелинейные и учет этих нелинейностей принципиально необходим, то используют кусочно-линейные модели. Этот метод часто используется для моделирования СИП.

Среди известных нелинейных моделей СПП используются фи­зические и функциональные модели. К наиболее точным моделям относятся модели Эберса-Молла, Агаханяна, Линвилла и др. Эф­фективность их применения зависит от типа решаемых задач и вида исследуемых процессов в преобразователях. При расчете электромагнитных процессов в цепях нагрузки преобразователей, коммутационных контурах и других силовых цепях достаточно воспользоваться более простыми моделями СПП, позволяющими при достаточной точности существенно уменьшить объем вычис­лений. К таким функциональным моделям относятся кусочно-ли­нейные, обеспечивающие замену реальной ВАХ СПП ее кусочно-линейной аппроксимацией. Наибольшее распространение среди них имеют модели на основе аппроксимации ВАХ двумя отрезками прямой, которые получили название ключевых моделей или S-uo-делей [1]. Ключевые модели отражают функционирование СПП как ключа с двумя состояниями (замкнут, разомкнут), переход между которыми осуществляется мгновенно. Такой ключ, сопро­тивление которого равно нулю в замкнутом состоянии и беско­нечности в разомкнутом состоянии, называется идеальным ключом

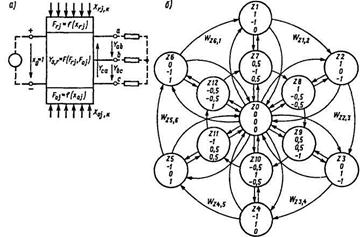
Рассмотренные ниже методы расчетов ориентированы на примене­ние ключевых моделей СПП, Модели цепей преобразователей, содержащих СПП. Силовые полу­проводниковые приборы, представленные в виде ключевых моделей, на основе теории автоматов предложено [5] заменить эквивалентными комбинационными автоматами, служащими для преобразования ин­формации о состоянии СПП в двоичном структурном алфавите (0 — ключ разомкнут, 1 — ключ замкнут). Полупроводниковые преобразо­ватели без накопителей энергии в силовых цепях, представляющие собой заданную композицию конечных автоматов, можно моделиро­вать в виде комбинационной схемы (рис. 5.2, а)

Состояние комбинационной схемы Z, определяется набором значе­ний входных функций состояния СПП F_rj, F_oj, например, главных тиристоров и обратных диодов автономного инвертора напряжения (см. гл. 9), и оценивается значениями функций выхода Y_rs схемы преобразователя. Анализ комбинационной схемы преобразователя, например, трехфазного автономного инвертора напряжения, показы­вает, что в нормально функционирующем инверторе имеются 72 на­бора (сочетания) значений функций для шести тиристоров F_rj и шести диодов F_oj, которым соответствуют 13 различных состояний схемы. Каждому состоянию схемы соответствует вполне определенное значе­ние функций выходных напряжений Y_rs {Y_ab, Y_bc, Y_ca}. В некотором структурном алфавите Ф, включающем в себя в рассматриваемом

Рис. 5.2. Комбинационная схема модели преобразователя (автономного инвертора напряжения) (а) и автоматное описание в форме графа комбинационной схемы (б)

примере символы {0; 0,5; 1; -1; -0,5}, это позволяет задать функцио­нирование преобразователей в рамках теории комбинационных схем автоматными описаниями.

На рис. 5.2, б представлен пример автомагного описания комбина­ционной схемы автономного инвертора напряжения в форме граф-схемы. Вершина графа соответствует состояниям схемы, а дуги — функциям перехода W_zkJ схемы из предыдущего состояния к в после­дующее состояние у. В случае простого алгоритма переключения ти­ристоров и диодов трехфазного инвертора одновременно замкнуты СПП трех плеч силовой схемы, поэтому Y_rsЄ[0; -1,1] и набор возмож­ных состояний Z₁—Z₆, что соответствует переходу от состояния к со­стоянию по наружным дугам графа. При более сложных алгоритмах многократного переключения СПП на одном периоде возможны дру­гие состояния схемы (Z₇, Z₁₂, Z₁₃) и траектории переходов.

W_zkj⁼ (F_r(j-l) F_r(j-2) + Fo(j-1) Fo(j-2)) (Frj + FoJ) + Fo(j-1) Foj F_r(j-2) + F_r(j-1)Fo(j-2)Frj, (5.1)

Функция перехода комбинационной схемы для простого алгорит­ма, когда возможные состояния включают в себя Z₁—Z₆ с переходами по наружным дугам графа, имеет вид

где j — число, соответствующее номеру интервала длительностью π/3 на рассматрива­емом периоде и обегающее кольцевую последовательность чисел 1, 2, 3, 4, 5, 6; к =j-1.

В зависимости от заданной частоты переключений СПП в схеме, значений токов в цепях нагрузок i_a,_b,с и времени t находятся значения переключательных функций F_rj и F_0j для заданного алгоритма их переключений. По их значениям с помощью функции перехода схемы W_z определяется состояние комбинационной схемы Z_i, которому ста­вится в соответствие набор значений выходных переменных Y_rs (на графе рис. 5.2, б проставлены в кружках вершин). Такое представле­ние схемы преобразователя позволяет создавать математические мо­дели сложных систем тягового электропривода и выполнять вычисли­тельные эксперименты на ЭВМ, что существенно сокращает затраты на исследование.

Дата добавления: 2014-01-07