ЛЕКЦИЯ 4. Выборка, когда все поставленные на испытания объекты доработали до отказа, т

Выборка, когда все поставленные на испытания объекты доработали до отказа, т. е. закончили испытания, называется полной. Если же испыта-ния прекращены до того, как все изделия в выборке отказали, то последняя на-зывается усеченной.

Покажем порядок определения важного показателя надежности, с помощью которого оценивается безотказность, — средней наработки до первого отказа (математическое ожидание наработки до первого отказа):

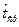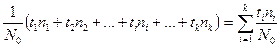=, (4)

где k- число интервалов.

Так как число отказов в интервале n_i называют весом, то определенное нами значение i называется средневзвешенным (смысл значка ^ будет объяснен дальше).

По мере увеличения наработки возрастает число отказавших изделий и убывает соответственно число работоспособных.

Подсчитаем накопленное число отказов r (t_i) как сумму отказов в интер-валах и соответственно число остающихся работоспособными изделий N(t_i).

Очевидно, что: r(t_i)+N(t_i) =N₀. (5)

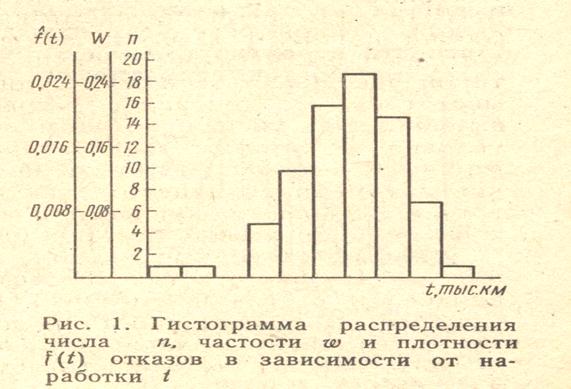
Изобразим графически изменение числа отказов от интервала к интервалу. Получим столбчатый график, который называется гистограммой (рис. 1).

Более полное, а главное, обобщенное представление о надежности дают не абсолютные, а относительные (удельные) значения полученных данных. Так, вместо абсолютных значений числа отказов в интервале n_i целесообразно подсчитать отношение ω_i=n_i/N₀, (6)

т. е. долю отказов в интервале, приходящуюся на одно и изделии из числа находящихся под наблюдением. Это отношение называется частостью.

Если разделить частость на длину интервала Δt, то получим долю отказов в интервале, приходящуюся на одно испытываемое изделие и на единицу наработки, т. е.на одну тысячу километров пробега. Эта удельная величина

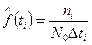(7)

называется оценкой плотности вероятности наступления отказа (оценка плотности распределения наработки до отказа). Так как для данного примера величины ∆t и N₀ постоянны, то высоты столбиков гистограмм n_i, ω_i и f(t_i) отличаются только масштабом.

Средняя наработка до отказа t_ср может быть определена из формулы (4),следующим образом:

,

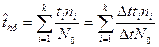Так как

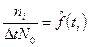, то .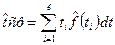

Для получения вероятностной характеристики t_ср переходим к пределу. Получим:

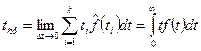. (19)

Так как 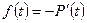, то

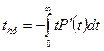(20)

Известно, что в теории вероятностей средняя величина называется математическим ожиданием. Таким образом формулы (13) и (14) дают возможность определить математическое ожидание наработки до первого отказа.

Проинтегрируем по частям:

;

;

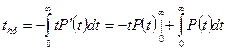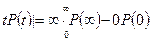Р(∞) =0, так как при неограниченной наработке (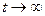) все изделия по истечении определенного периода откажут; Р(0)=1, так как в начале эксплуатации (t =0) отказов еще нет и вероятность безотказной работы равна единице.Что касается неопределенности ∞▪Р(∞), то не очень строго (рис. 4) можно заключить, что Р(t) стремится к нулю быстрее (кривая имеет крутизну), чем. (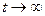). Отсюда в нашем случае ∞•0=0, и тогда получаем другое выражение для математического ожидания:

или, (21) где 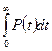есть площадь под кривой Р(t).

Величину t_ср можно определить по площади под кривой Р( t) на рис. 4 с учетом масштаба. Из этого следует, что при вероятности безотказной работы, выраженной на рис. 4 кривой 1, средняя наработка до первого отказа больше, чем в двух других случаях.

В некоторых источниках дано несколько иное трактование показателей безотказности.

Невосстанавливаемые объекты. Для опреде.цения показателей безотказности необходимо знать распределение отказов как случайных событий. Распределение описывается характеристиками плотности распределения (плотности вероятности) отказов f(х), интегральной функцией (вероятности) распределения отказов F(х), вероятностью безотказной работы (кривой убыли) R(х). Первые две характеристики связаны следующей зависимостью:

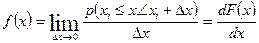(1)

Отсюда следует, что произведение f(х)Δх при достаточно малом Δх приблеженно равно вероятности нахождения х в интервале от х_i, до х_i + Δх, что записывается условно:

р (х₁ ≤х < х₁ + Δх).

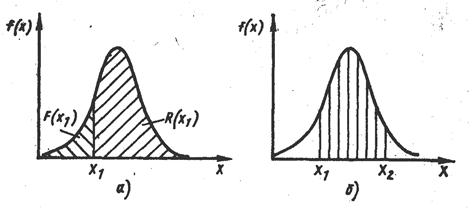
Рис. 1. Кривые плотности вероятностей

С помощью плотности распределения можно найти вероятность появления отказа при наработке х, не превышающей требуемой х₁

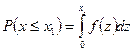, (2)

где z — переменная интегрирования. Выражение (2) можно истолковать графически: вероятность появления отказа за наработку х, меньшую требуемой х₁ равна относительной площади под кривой f(х) слева от значения х₁ (рис. 1, а).

Плотность распределения позволяет найти и величину, проти воположную F(х), т. е. вероятность безотказной работы R(х). Полагая, что изделие может быть только в одном из двух состояний—отказа или работоспособности, запишем: R(x₁) + F(x₁) =1. Отсюда

R(x₁) = р (х > x₁) = 1— F (х₁) = (3)

Вероятность безотказной работы, т. е. того, что наработка х до отказа будет больше требуемой х₁ равна относительной площади под кривой f(х) справа от значения х₁. Плотность распределения позволяет найти вероятность того, что случайная величина х заключена между х₁ и х₂ (рис. 1, б):

р (х₁ ≤х < х₂) = F (х₂) — F (х₁) = - = .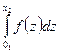

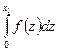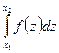Наконец, плотность распределения позволяет найти среднюю наработку до отказа:

х_ср =

Функции распределения f(х),R(х) и F(х) связаны между собой формулами (1)—(3). Интегральные функции R(х) и F(х) могут быть представлены в виде графиков (рис. 2).

Рис. 2. Функции распределения Рис. 3. Изменение интенсивности от-

казов в зависимости от наработки:

Г. с. — гарантийный срок; Р — ресурс

Если известна наработка х_i то по кривым можно опрёделить две вероятности: F (х) — появления отказа (потери работоспособности) и R (х) — безотказной работы, все при х < х_i

Для ряда расчетов удобно рассматривать функцию, дающую вероятность отказа за очень короткий промежуток времени. Так как рассматриваются невосстанавливаемые объекты, естественно условие отсутствия отказов рассматриваемого момента времени. Эта функция называется интенсивностью отказов

λ(х) = f(х) / Р(х) (4)

Произведение λ(х)·Δх— это доля элементов, которые безотказно работали до наработки х и, вероятно, выйдут из строя при наработках в пределах от х до х+Δх. Вид функции интенсивности отказов приведен на рис. 3.

Разделим наработку на три периода.

Период 1 — приработка, когда интенсивность отказов повышена из-за ранних или приработочных отказов, обусловленных дефектами производства. Иногда с окончанием этого периода связана гарантийная наработка (гарантийный срок), когда устранение отказов и восстановление роботоспособности производятся за счет завода-изготовителя. Гарантийная наработка и гарантийный срок устанавливаются по договоренности между изготовителем и заказчиком.

Период II — нормальная эксплуатация, отличающаяся минимальной величиной λ(х). Часто интенсивность отказов за этот период можно принимать почти постоянной, что существенно упрощает все расчеты.

Период III — выход в предельное состояние, когда начинаются отказы в результате интенсивного износа, усталостных разрушений, старения и других причин, обусловленных длительностью эксплуатации

Точные значения показателей безотказной работы определают по формулам, приведенны выше. При испытаниях или наблюдениях в эксплуатации получают приближенные (статистические) их значения, представляющие оценку точных. Чем больше объем опытных данных, тем ближе приближенное значение к точному, тем точнее его оценка.

Для приближенного определения показателей безотказности необходимо знать (для испытуемых или наблюдаемых в. эксплуатации объектов) их наработки до отказа или до конца наблюдений (испытаний): х₁, х₂,..., х_n. Тогда вероятность появления откааа при наработке х₀, когда отказало N’ изделий и сохранило работоспособность N^" = N - N’ изделий, равна

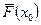= N’/ N (5)

Здесь и далее приближенные (статистические) оценки будем обозначать теми же буквами, но с черточками сверху.

Вероятность безотказной работы

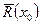= N^"/ N (6)

Вероятность безотказной работы R является удобным оценочным показателем, Однако для высоконадежных изделий целесообразнее пользоваться ероятностью F= 1— R или производными величинами — числом отказов на одно изделие, на 1000 изделий и т. д.

Средняя наработка до отказа — это отношение суммы наработки испытуемых объектов до отказа к их числу. Оценка средней наработки до отказа зависит от плана испытаний и закона распределения наработки до отказа. Если наблюдается N объектов и все они отказывают, то средняя наработка до отказа составит

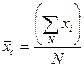(7)

Если из N наблюдаемых объектов за время t отказало r объектов, то средняя наработка до отказа будет равна

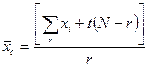. (8)

Интенсивность отказов, соответствующая достаточно малому интервалу времени Δt (малой наработке Δх),

, (9)

где ΔN —число отказавших объектов за наработку Δх; N—число работоспособных объектов к началу рассматриваемой наработки.

Таким образом, интенсивность отказов прибляженно равна числу отказов, отнесенному к единице наработки и числу объектов.

Восстанавливаемые объекты. В простейшем случае работа N восстанавливаемых объектов отличается тем, что при возникновении отказов, происходит восстановление и работа объектов продолжается. Таким образом, имеем N = const число отказов m < > N в потоках отказов и восстановлений, сопровождающих работу объектов.

Потоки отказов необходимо знать не только для оценки безотказности объекта. Они определяют потоки восстановления, важные для расчета ремонтных средств. Поток отказов характеризуется следующими величинами: средним числом отказов m_c(х) и параметром потока отказов ω(х). Если каждый из объектов при наработке х имеет m_i (х) отказов, то среднее число отказов, соответ ствующее наработке х, будет равно

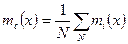(10)

Введем понятие характеристики потока отказов Н(х) — предела, к которому стремится среднее число отказов при N→ ∞:

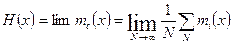(11)

Протекание функции Н (х) зависит обычно от периода эксплуатации объекта. В период приработки функция Н(t) может убывать, а при нормальной эксплуатации — возрастать. Интенсивность изменения характеристики потока отказов во времени была названа параметром потока отказов; его точное значение

Параметр потока определяет среднее число отказов в единицу времени вблизи наработки х. Приближенно параметр потока отказов по их количеству за наработку (обычно достаточно малую) Δх равен

(13)

Если F(х) — вероятность появления отказа в интервале от х₁ до х₂ то параметр потока отказов определяется по следующей формуле:

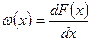(14)

Отсюда следует, что параметр потока отказов за наработку х равен вероятности отказа объекта на единицу наработки в единицу времени. Для сложных изделий суммарный поток отказов равен сумме потоков отказов составляющих элементов:

m_с0(х) = m_с1(х) + m_с2(х) +... + m_сN(х).

Дифференцируя по х, находим

ω(х) = ω₁(х) + ω₂(х) +... + ω_N(х). (15)

Таким образом, параметр суммарного потока отказов равен сумме параметров составляющих потоков. Для автомобилей и их агрегатов принято определять численные значения параметров потока отказов с учетом наработки с начала эксплуатации. Размерность параметра потока отказов определяется размерностью наработки. Это может быть 1/км, 1/ч и т. д. Понятие характеристики потока отказов позволяет дать более общее уравнение для определения наработки на отказ для периода х₁ – х₂

х = (х₂ — х₁) /[Н(х₂) — Н (х₁)] (16)

или приближенно

х ≈ (х₂ — х₁) /[m_с(х₂) — m_с (х₁)] (17)

Распространенный вид потока отказов называется стационарным, ординарным, не имеющим последействий.

Поток является стационарным, если число отказов зависит от величины наработки х₂ — х₁ и не зависит от величины х₁ или х₂. Так, в период приработки поток отказов, как правило, не является стационарным, зато в период нормальной эксплуатации часто его можно считать стационарным. Это значит, что Н(х) в период II (рис. 3) становится линейной функцией и описывается уравнением

Н(х) = Н(х₀) + ω(х – х₀) (18)

Здесь х₀ соответствует времени приработки. Параметр стационарного потока отказов является постоянной величиной.

Для того чтобы Н(х) была линейной функцией, а ω — соnst одного условия стационарности недостаточно. Необходимо, чтобы отказы возникали по одному и не обусловливали взаимного появления, т. е. должно соблюдаться требование ординарности без последействия.

Поток отказов является ординарным, если при любой наработке одновременно возникает не более одного отказа. Наконец, в потоке отказов должно отсутствовать последействие: отказ одних элементов не должен приводить к отказу других и менять параметр потока. Это ограничение не всегда справедливо, так как отказы одних элементов могут вызвать отказы других, с ними связанных; отказ одного элемента может вызвать также опасные перенапряжения и скрытые повреждения других элементов, приводящие позже к их отказам и, следовательно, влиящие на параметр потока.

Принятые характеристики потока означают, что появления двух или более отказов в один и тот же момент времени. ничтожно мала, вероятностный режим не меняется во времени и протекание потока после любого момента времени не за висит от его характера до этого момента.

\Т

Если для каждого значения парамера х=х₀ вероятность любого состояния системы в будущем для интервала наработки х₀ - (х_о+Δх) зависит только от состояния системы в начальный момент, соответствующий х₀ и не зависит от того, каким образом система пришла в это первоначальное состояние, то такой случайный процесс называется марковским (или процессом без последействия).

Сравнивая формулы (9) и (13), можно заключить, что понятия интенсивности отказов λ(х) для невосстанавливаемого объекта и параметра потока отказов ω (х) для восстанавливаемого объекта родственны. В случае ординарного потока без последействия они совпадают.

Дата добавления: 2014-01-07