И способы расчёта

ВОПРОС 17: СТРУКТУРНЫЕ СРЕДНИЕ, ИХ ВИДЫ, НАЗНАЧЕНИЕ

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода – это значение случайной величины, встречающейся с наибольшей вероятностью в дискретном вариационном ряду, т. е. вариант, имеющий наибольшую частоту. В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:

,

где 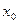- нижняя граница модального интервала;

- величина модального интервала;

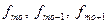- соответственно частоты модального, предмодального и послемодального интервала.

Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т. п.

Медиана – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные по числу единиц части – со значениями признака меньше медианы и со значениями признака больше медианы.

В дискретных вариационных рядах нахождение медианы сводится к отысканию порядкового номера медианы. Номер медианы для нечётного объёма вычисляется по формуле:

№

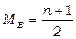
В случае четного объёма ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медиана оказывается в каком-то из интервалов признака. Этот интервал характерен тем, что его кумулятивная частота (накопительная сумма частот) равна или превышает полусумму всех частот ряда.

,

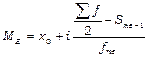где 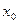- нижняя граница медианного интервала;

- величина медианного интервала;

- полусумма частот;

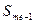- накопительная частота до начала медианного интервала;

- частота медианного интервала.

Структурные средние являются конкретными характеристиками. Мода и медиана отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.

Дата добавления: 2014-01-07