Вопрос 24: регрессионный Метод анализа связи

Задачи статистики в области изучения взаимосвязей состоят в количественной оценке их наличия, направления и силы связи, в определении формы влияния факторных признаков на результативный. Для решения этих задач применяют методы корреляционного и регрессионного анализа. Корреляция и регрессия тесно связаны между собой: первая оценивает силу (тесноту) статистической связи, а вторая исследует ее форму. Та и другая служат для определения наличия или отсутствия связи между явлениями.

Задачи регрессионного анализа:

· выбор типа модели (формы связи);

· установление степени влияния независимых переменных на зависимую переменную;

· определение расчетных значений зависимой переменной (функции регрессии).

По форме зависимости различают:

1 линейную регрессию, которая выражается уравнением прямой: ;

2 нелинейную регрессию, которая выражается уравнениями:

параболы: ;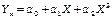

гиперболы: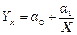и т.д.

Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться эмпирически – перебором и оценкой разных типов. В частности, если результативный и факторный признаки возрастают примерно в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи – гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный – значительно быстрее, то используется параболическая или степенная регрессия.

Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов:

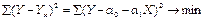
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:

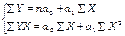
Решим эту систему в общем виде:

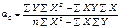
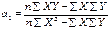
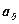- усредненное влияние на результативный признак неучтенных факторов	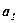- коэффициент регрессии, показывающий, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения

Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:

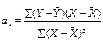или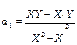

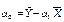
Определив значения a₀, a₁ и подставив их в уравнение связи 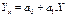, находим значения Y_x, зависящие только от заданного значения Х.

По такому же принципу решается уравнение связи при криволинейной зависимости между изучаемыми явлениями. Если зависимость принимает форму параболы второго порядка, то для записи такой зависимости используют уравнение: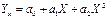

Задача сводится к нахождению параметров a₀; a₁; a₂. Для этого необходимо решить систему трех корреляционных уравнений:

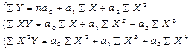
Решая систему и определив значения неизвестных коэффициентов a₀; a₁; a₂, получим искомое уравнение регрессии.

Довольно часто в экономическом анализе для криволинейных зависимостей используется гипербола:

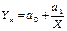
Для определения ее параметров необходимо решить следующую систему уравнений:

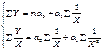
Таким образом, используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, т.е. узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением факторного на единицу.

Дата добавления: 2014-01-07