
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы отражения
|
|
|
|
Рассмотрим законы отражения упругих волн, воспользовавшись принципом Ферма. Пусть в пласте I в точке 0 расположен источник, от которого во все стороны распространяется волна со скоростью V (рис. 2.2).
(рис. 2.2).




 О С
О С
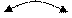
 I d
I d 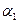
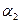 b
b

 x
x
В

a
Рис. 2.2. Отражение волны
На границе образуется отраженная волна распространяющаяся в слое I со скоростью V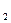 . В случае монотипной отраженной волны V
. В случае монотипной отраженной волны V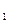 = V
= V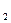 , в случае обменной отраженной волны V
, в случае обменной отраженной волны V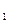
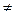 V
V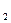 . Предположим, что луч падающей волны достигает границу раздела в точке В, а отраженная волна выходит в точку С. Положение точки В выбрано произвольно. Совместим с границей раздела ось координат x. Тогда рассматриваемые точки имеют координаты: О(0, d), В(x,0), С(a, b). Определим время пробега волны – t вдоль луча ОВС:
. Предположим, что луч падающей волны достигает границу раздела в точке В, а отраженная волна выходит в точку С. Положение точки В выбрано произвольно. Совместим с границей раздела ось координат x. Тогда рассматриваемые точки имеют координаты: О(0, d), В(x,0), С(a, b). Определим время пробега волны – t вдоль луча ОВС:
t=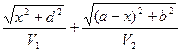 . (2.1)
. (2.1)
По принципу Ферма точка В должна быть расположена так, чтобы время пробега волны по лучу было наименьшим. Определим значение координаты x при которой выполняется это требование, приравняв к нулю производную 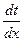 :
:
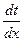 =
=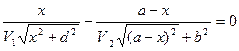 . (2.2)
. (2.2)
Согласно рис. 2.2,

Sin 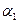 =
= ; Sin
; Sin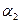 =
=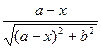 , (2.3)
, (2.3)
где 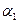 - угол падения,
- угол падения, 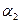 - угол отражения. Тогда из уравнения (2.2) получим:
- угол отражения. Тогда из уравнения (2.2) получим:
 . (2.4)
. (2.4)
Это соотношение выражает закон отражения (закон Снеллиуса) в общей форме, который справедлив для обменных волн. В случае отражения монотипной волны, когда V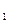 = V
= V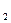 получим
получим
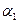 =
=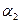 , (2.5)
, (2.5)
т.е. угол отражения равен углу падения.
Рассмотрим зависимость между амплитудами отраженной и падающей волн вблизи границы раздела двух сред. Пусть а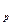 - амплитуда падающей продольной волны Р
- амплитуда падающей продольной волны Р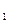 , а
, а - амплитуда отраженной продольной волны Р
- амплитуда отраженной продольной волны Р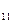 , а
, а - амплитуда отраженной поперечной волны Р
- амплитуда отраженной поперечной волны Р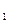 S
S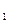 . Соотношения:
. Соотношения:
A =
=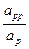 , A
, A =
=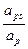 , (2.6)
, (2.6)
Называются коэффициентами отражения. Они определяют амплитуды отраженных волн сравнительно с амплитудой падающей волны. Коэффициенты отражения сложным образом зависят от угла падения  , скоростей и плотностей в средах, прилегающих к границе раздела. В случае нормального падения, когда луч перпендикулярен границе и, следовательно,
, скоростей и плотностей в средах, прилегающих к границе раздела. В случае нормального падения, когда луч перпендикулярен границе и, следовательно,  = 0 коэффициенты отражения соответствуют следующим выражениям:
= 0 коэффициенты отражения соответствуют следующим выражениям:
A =
= , A
, A =0. (2.7)
=0. (2.7)
Произведение  называют волновым сопротивлением или акустической жесткостью среды. Из уравнения (2.7) видно, что отраженная волна образуется при условии:
называют волновым сопротивлением или акустической жесткостью среды. Из уравнения (2.7) видно, что отраженная волна образуется при условии:
 . (2.8)
. (2.8)
Следовательно, отраженные волны образуются на границах пластов с различными волновыми сопротивлениями. Такие границы называют отражающими. Чем больше различие волновых сопротивлений по обе стороны отражающей границы, тем больше амплитуда отраженной от неё волны. Из формулы (2.7) видно, что при нормальном падении луча (  = 0), возникают только монотипные отраженные волны. Обменная отраженная волна образуется, когда угол падения отличен от нуля. Существуют специальные таблицы и графики, при помощи которых можно определить коэффициенты отражения волн при различных углах падения.
= 0), возникают только монотипные отраженные волны. Обменная отраженная волна образуется, когда угол падения отличен от нуля. Существуют специальные таблицы и графики, при помощи которых можно определить коэффициенты отражения волн при различных углах падения.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 274; Нарушение авторских прав?; Мы поможем в написании вашей работы!